数据结构中栈的使用
1 栈
1.1 应用场景
- 计算器实现:
- 将一个数学算术字符串,例
1+2*3+4/5,计算出来其正确结果来 - 底层的实现运用到了栈数据结构
- 其他场景:
- (1)子程序的调用:在跳往子程序前,会先将下一个指令的地址存储在栈中,直到子程序执行完后再讲地址取出,以回到原来的程序中
- (2)处理递归调用:和子程序的调用类似,只是处理存储下一个指令的地址外,也将参数、区域变量等数据存入栈中
- (3)表达式的转换(中缀表达式转后缀表达式)与求值
- (4)二叉树的遍历
- (5)图形的深度优先搜索法
1.2 介绍
- 栈的英文为
Stack - 栈是一个先进后出(FILO:First In Last Out)的有序列表
- 栈是限制线性表汇元素的插入与删除,只能在线性表的同一段进行的特殊线性表。允许添加与删除的一端,为栈顶(top),固定的另一端为栈底(Bottom)
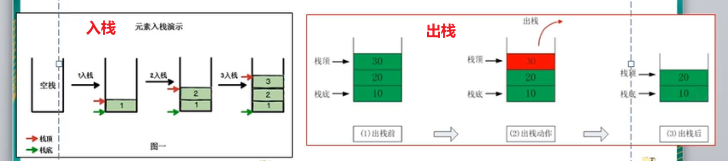
1.3 代码实现
- (1)思路
- 栈底为bottom,永远为0;栈顶为top,是当前数据的index + 1;
- 入栈:
stack[top] = data; top++;,栈顶赋值,然后再移动栈顶 - 出栈:
top--; data = stack[top];,栈顶先减一,移动到最新数据的index,在取出数据 - 满栈:
top == size,栈顶等于栈的大小 - 空栈:
top == bottom,栈顶 等于 栈底
- (2)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57public class ArrayStack {
private int size; //栈的大小
private int top; //栈顶(最新数据index + 1)
private int bottom; //栈底(永远为0)
private int[] stack; //栈
public ArrayStack(int size) {
this.size = size;
stack = new int[size];
top = 0;
bottom = 0;
}
/**
* 入栈
* @param data 数据
*/
public void push(int data) {
//判断是否满栈
if(size == top) {
System.out.println("栈已满,无法添加数据");
}else {
stack[top++] = data; //先赋值,再top+1
}
}
/**
* 出栈
* @return int
*/
public int pop() {
//判断是否空栈
if(top == bottom) {
System.out.println("栈为空,没有数据可取!");
return 0; //暂时以0为取值失败
}
return stack[--top]; //先top-1,在返回数据
}
/**
* 打印栈
*/
public void print() {
if(top == bottom) {
System.out.println("栈为空!");
}
int temp = top;
System.out.println("数组栈为:");
while (temp != bottom) {
temp--;
System.out.println(stack[temp]);
}
}
}
- (3)测试
1
2
3
4
5
6
7
8
9
10
11
12
13
public void arrayStackTest() {
//1. 创建栈并入栈
ArrayStack stack = new ArrayStack(3);
stack.push(1);
stack.push(2);
stack.push(3);
stack.print();
//2. 出栈
stack.pop();
stack.print();
}

1.4 拓展:链表实现栈
由于链表的长度没有限制,可以无限添加,所以链表栈没有满栈的概念
(1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73public class LinkedListStack {
//节点类
private class Node {
public int data;
public Node next;
public Node(int data) {
this.data = data;
}
public String toString() {
return "Node{ data = " + data + " }";
}
}
private Node headNode; //头节点
public LinkedListStack() {
headNode = new Node(0);
}
/**
* 入栈(头插法)
* @param data 数据
*/
public void push(int data) {
Node node = new Node(data);
node.next = headNode.next;
headNode.next = node;
}
/**
* 出栈(返回并删除第一个节点)
*/
public int pop() {
if(isEmpty()) {
System.out.println("error:栈为空,没有数据可取!");
return 0; //暂时以0作为错误返回
}
Node temp = headNode.next;
headNode.next = headNode.next.next;
return temp.data;
}
/**
* 打印链表栈
*/
public void print() {
if(isEmpty()) {
System.out.println("链表为空!");
return;
}
System.out.println("链表栈为:");
Node temp = headNode.next;
while (temp != null) {
System.out.println(temp);
temp = temp.next;
}
}
/**
* 判断是否空栈
* @return boolean
*/
public boolean isEmpty() {
return headNode.next == null;
}
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
11
12
13
public void linkedListStackTest() {
//1. 创建栈并入栈
LinkedListStack stack = new LinkedListStack();
stack.push(1);
stack.push(2);
stack.push(3);
stack.print();
//2. 出栈
stack.pop();
stack.print();
}

2 计算器实现
2.1 基础版(存在bug)
- (1)思路
- 创建两个栈,一个栈用来存数字,一个栈用来存字符
- 将字符串转为字符数组,然后遍历字符串
- 遍历到数字就加入数字栈
- 遍历到操作符,需要进行分析;
- 操作符栈为空,直接添加;
- 操作符优先级大于栈顶操作符的优先级,直接添加;
- 操作符优先级小于栈顶操作符的优先级,取出操作符栈顶数据,以及数字栈的两个数据,进行计算,将计算结果push回数字栈,然后才push要新增的操作符
- 遍历完毕后,取操作符进行计算,直到操作符栈为空,则数字栈的结果为最终结果
- (2)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119public class Calculator {
private LinkedListStack numStack; //数字栈(自定义链表栈)
private LinkedListStack operateStack; //操作符号栈(自定义链表栈)
public Calculator() {
numStack = new LinkedListStack();
numStack.push(0); //防止表达式负数开头
operateStack = new LinkedListStack();
}
/**
* 计算表达式并打印结果
* @param express 表达式
*/
public void calculateExpress(String express) {
//字符串转字符数组
char[] chars = express.toCharArray();
//遍历字符数组进行入栈
for(char c : chars) {
//判断数字or操作符
if(c >= '0' && c <= '9') {
int i = Integer.parseInt(String.valueOf(c)); //字符数字为ascii值,需要转换整型
numStack.push(i);
}else {
pushOperateStack(c);
}
}
//入栈完毕进行计算出栈
while (!operateStack.isEmpty()) {
char operate = (char) operateStack.pop();
int num1 = numStack.pop();
int num2 = numStack.pop();
int data = calculate(num1, num2, operate);
numStack.push(data);
}
//操作符栈为空,直接返回数字栈数据
System.out.printf("表达式的结果为:%d", numStack.pop());
}
/**
* 往操作符栈进行入栈
* @param c 字符
*/
private void pushOperateStack(char c) {
if (operateStack.isEmpty()) {
//栈为空,直接入栈
operateStack.push(c);
}else {
//栈非空,判断栈顶符号,与传入符号的优先级
char operate = (char) operateStack.pop();
if (getPriority(c) > getPriority(operate)) {
// 优先级 > 栈顶的操作符,入栈
operateStack.push(operate);
operateStack.push(c);
}else {
// 优先级 < 栈顶操作符, 计算栈顶,再入栈
int num1 = numStack.pop();
int num2 = numStack.pop();
int data = calculate(num1, num2, operate);
numStack.push(data);
operateStack.push(c);
}
}
}
/**
* 获取操作符的优先级
* @param c 操作符
* @return int
*/
public int getPriority(char c) {
switch (c) {
// + 和 - 优先级为 1
case '+':
case '-':
return 1;
// * 和 / 优先级为 2
case '*':
case '/':
return 2;
default:
throw new RuntimeException("error:非法操作符!");
}
}
/**
* 数字计算
* @param num1 数字1
* @param num2 数字2
* @param operate 操作符
* @return int
*/
private int calculate(int num1, int num2, char operate) {
int data = 0;
switch (operate) {
case '+':
data = num1 + num2;
break;
case '-':
data = num2 - num1;
break;
case '*':
data = num1 * num2;
break;
case '/':
if (num1 == 0) {
throw new RuntimeException("error:0不能作为分母!");
}
data = num2 / num1; //暂时'/'以整型接受
}
return data;
}
}
- (3)测试
1
2
3
4
5
public void calculatorTest() {
Calculator calculator = new Calculator();
calculator.calculateExpress("3+2*6-2");
}
- (4)存在bug
- 只能计算个位数的数字,否则计算出错
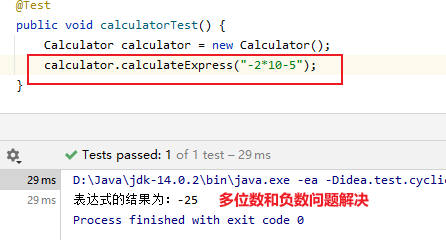
- 负数计算存在一定的问题,例:
-2*5-5,按道理是计算出-15,但是上述算法无法识别负号之间是相加的,直接变成10-5,然后再0-5,算出-5
2.2 改进版
- (1)思路
- 多位数问题,可以定义一个中间变量,读取的是数字,就存在中间变量中,不立马入栈。直到读取到操作符时,再进行入数字栈。还有最后一个数字后面没有操作符,所以读取字符数组后,还要将中间变量进行入栈
- 减法问题:可以将减法改变为加法,加负数的形式
- (2)bug解决
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38// //遍历字符数组进行入栈
// for(char c : chars) {
// //判断数字or操作符
// if(c > '0' && c < '9') {
// int i = Integer.parseInt(String.valueOf(c)); //字符数字为ascii值,需要转换整型
// numStack.push(i);
// }else {
// pushOperateStack(c);
// }
// }
//改进版
String temp = "";
for(char c : chars) {
//判断数字or操作符
if(c >= '0' && c <= '9') {
//在temp中存储字符,不立刻入栈,解决多位数问题
temp += c;
}else {
//入数字栈并清空temp
if(temp != "") {
numStack.push(Integer.parseInt(temp));
temp = "";
}
//如果是减法,转变成加法 +负数的形式
if (c == '-') {
temp += '-';
c = '+';
}
pushOperateStack(c);
}
}
//表达式最后的数字需要从temp中入数字栈
numStack.push(Integer.parseInt(temp));
3 前中后缀表达式
3.1 前缀表达式
3+4x5-6的前缀表达式为:- + x 4 5 3 6- 操作符在前面,数字在后面
- 优先级高的操作符在后面,对应操作符参与运算的数字放前面
- 计算机扫描前序表达式为:从右到左,
- 例:所以数字依次进栈为
[4 5 3 6],读取到操作符x,就取数字栈前两个数字,4x5=20,将20放入数字栈[20 3 6];依次类推,计算得出结果
- 例:所以数字依次进栈为
3.2 中缀表达式
3+4x5-6的中缀表达式就是我们平时熟悉的表达式3 + 4 x 5 - 6- 我们前面的计算器的演示就是使用中缀表达式来完成
- 对于人来说很容易理解,但对于计算机来说不好理解,一般都是转变成后缀表达式进行计算
3.3 后缀表达式(逆波兰表达式)
3+4x5-6的后缀表达式为:3 4 5 x + 6 -- 参与运算的两个数字放前面,操作符放后面
- 所以一步步得出
4x5 = 4 5 x,3+4x5 = 3 4 5 x +,3+4*5-6 = 3 4 5 * + 6 - - 计算机扫描后缀表达式为:从左到右,遇到数字就入栈,遇到操作符就计算数字栈前两个数字,再将计算的结果入栈
- 例:数字入栈
[5 4 3],遇到操作符x,去数字栈两数字计算5x4=20,再结果放回栈[20 3],依次类推,计算出最终结果
- 例:数字入栈
3.4 中缀转后缀表达式
- (1)创建两个栈,一个栈S1主要存数字(也会存运算符),另一个栈S2存运算符
- (2)从左到右遍历中缀表达式
- (3)读取到数字,则压入数字栈
- (4)读取到非数字时,进行判断:
- 运算符栈S2为空,直接入栈
- 入栈运算符 > 栈顶运算符,直接入栈
- 入栈运算符 < 栈顶运算符,取出栈顶运算符并入栈到数字栈S1,在将运算符入栈S2
(,遇到左括号直接入栈
),遇到右括号,将运算符号出栈S2,并入栈到数字栈S1,直到出栈的数据为(为止
- (5)所有数据遍历完毕后,判断符号栈S2是否有数据,有就出栈并入栈到数字栈S1,直到空栈为止
4 逆波兰计算器
- 我们用中缀转后缀的形式,创建一个后缀表达式的计算器
- (1)实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170public class PolandCalculator {
/**
* 中缀表达式转后缀表达式
* @param infixExpression 中缀表达式
* @return String
*/
public List<String> InfixToSuffix(String infixExpression) {
List<String> numStack = new ArrayList<>(); //数字栈(因为全程无需出栈,所以已一个集合来存储更方便)
Stack<Character> operateStack = new Stack<>();
char[] chars = infixExpression.toCharArray();
if(chars[0] == '-') {
//如果是负数开头,添加一个0入数字栈
numStack.add(String.valueOf(0));
}
//遍历
int count = 0; //记录第一个数字表示
String temp = "";
for (char c : chars) {
if (c >= '0' && c <= '9') {
temp += c; //中间变量解决多位数
}else {
if(temp.length() != 0) {
//数字入栈
numStack.add(temp);
temp = "";
}
//符号入栈
operatePush(operateStack, numStack, c);
}
}
numStack.add(temp); //将最后的数字入栈
//操作符号栈非空,入栈到数字栈
while (!operateStack.empty()) {
numStack.add(String.valueOf(operateStack.pop()));
}
return numStack;
}
/**
* 非数字符号入栈
* @param operateStack 运算符号栈
* @param numStack 数字栈(集合形式)
* @param c 符号
*/
public void operatePush(Stack<Character> operateStack, List<String> numStack, char c) {
String data;
//栈为空 或 栈顶为'(' 或 入栈符号为'(' 直接入栈即可
if (operateStack.empty() || operateStack.peek() == '(' || c == '(') {
operateStack.push(c);
return;
}
//入栈的为')',遍历出栈,并将出栈数据压入符号栈,直到出现'('为止
if (c == ')') {
while (operateStack.peek() != '(') {
numStack.add(String.valueOf(operateStack.pop()));
}
operateStack.pop(); //最后也要将'('出栈
return;
}
//非括号符号,比较优先级
if (getPriority(c) > getPriority(operateStack.peek())) { ;
//入栈符号 > 栈顶符号,直接入栈
operateStack.push(c);
return;
}else {
//入栈符号 <= 栈顶符号,出栈并压入数字栈
//栈不为空 并 入栈符号 <= 栈顶符号 持续出栈
while (!operateStack.empty() && getPriority(c) <= getPriority(operateStack.peek())) {
numStack.add(String.valueOf(operateStack.pop()));
}
operateStack.push(c);
return;
}
}
/**
* 获取操作符优先级
* @param c 操作符
* @return int
*/
public int getPriority(char c) {
switch (c) {
// + 和 - 优先级为 1
case '+':
case '-':
return 1;
// * 和 / 优先级为 2
case '*':
case '/':
return 2;
default:
throw new RuntimeException("error:非法操作符!");
}
}
/**
* 计算后缀表达式
* @param suffixExpression 后缀表达式
* @return Integer
*/
public Integer calSuffixExpression(List<String> suffixExpression) {
Stack<Integer> numStack = new Stack<>();
//遍历元素
for (String item : suffixExpression) {
//正则表达式匹配数字
if (item.matches("\\d+")) {
//数字,入栈
numStack.push(Integer.valueOf(item));
}else {
//非数字,计算结果,再入栈
Integer num1 = numStack.pop();
Integer num2 = numStack.pop();
//计算
Integer result = calculate(num1, num2, item);
numStack.push(result);
}
}
return numStack.pop();
}
/**
* 数字计算
* @param num1 参数1
* @param num2 参数2
* @param operate 运算符
* @return Integer
*/
public Integer calculate(Integer num1, Integer num2, String operate) {
Integer result = null;
//判断操作符,并进行相应计算
switch (operate) {
case "+":
result = num1 + num2;
break;
case "-":
result = num2 - num1;
break;
case "*":
result = num1 * num2;
break;
case "/":
result = num2 / num1; //暂时不考虑浮点型
break;
default:
throw new RuntimeException("error:非法操作符!");
}
return result;
}
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void PolandCalculatorTest() {
//计算公式(中缀表达式)
String ids = "-(7-4)-5"; //结果为-8
PolandCalculator polandCalculator = new PolandCalculator();
//中缀转后缀
List<String> strings = polandCalculator.InfixToSuffix(ids);
System.out.println(strings);
//计算后缀表达式
Integer integer = polandCalculator.calSuffixExpression(strings);
System.out.println(integer);
}
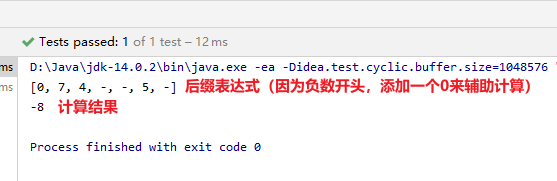
- 此计算器大部分功能都能实现了,但还是有一些bug,例如:小数不能解决,括号内第一个数为负数会计算出错
- 此bug解决就不展开说了,中缀转后缀的思想学到了就足够了,有机会可以自行解决