简单介绍递归,并实现一些递归常见问题
1 递归
1.1 递归介绍
- 递归就是方法自己调用自己,每次调用时传入不同的变量,递归有助于编程者解决复杂的问题,同时可以让代码变得简洁
1.2 递归图解介绍
- (1)简单递归代码
1
2
3
4
5
6
7
8
9
10
11
12
public void recursionTest() {
test(3);
}
public void test(int i) {
if(i > 1) {
test(i-1); //自己调用自己
}
System.out.println(i);
}
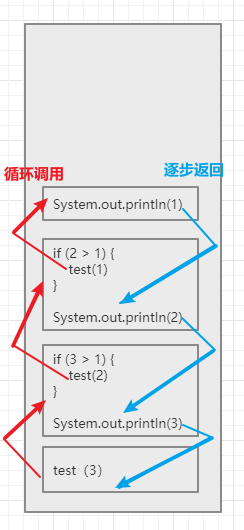
- (2)实现步骤图解
1.3 递归应用场景
- (1)8皇后问题
- (2)汉诺塔
- (3)阶乘问题
- (4)迷宫问题
- (5)球和篮子问题
- (1)快速排序算法
- (2)归并排序算啊
- (3)二分查找
- (4)分治算法
- 用栈解决的问题,可以用递归解决,代码相对简洁
1.4 递归规则
- (1)执行一个方法时,就创建一个新的受抱回的独立空间(栈空间)
- (2)方法的局部变量是独立的,不会相互影响
- (3)如果方法中使用的是引用类型变量,就会共享该应用类型的数据库
- (4)递归必须向退出递归的条件逼近,否则就是无限递归
- (5)当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕
2 应用:迷宫问题
2.1 问题
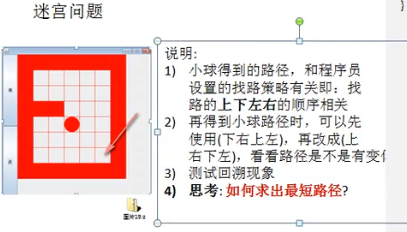
2.2 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97public class Maze {
private int[][] maze; //迷宫
public Maze() {
//创建对象时,自动创建迷宫
createMaze();
}
/**
* 创建迷宫(数组形式)
* 1表示墙壁,0表示可移动空间
*/
private void createMaze() {
maze = new int[8][7];
//上下创建围墙(设置为1)
for(int i=0; i<7; i++) {
maze[0][i] = 1;
maze[7][i] = 1;
}
//左右创建围墙(设置为1)
for(int i=0; i<8; i++) {
maze[i][0] = 1;
maze[i][6] = 1;
}
//中间墙壁(设置为1)
maze[3][1] = 1;
maze[3][2] = 1;
}
/**
* 查看迷宫
*/
public void viewMaze() {
System.out.println("当前迷宫为:");
for(int[] row : maze) {
for (int item : row) {
System.out.printf("%d\t", item);
}
System.out.println();
}
System.out.println();
}
/**
* 判断是否能走
* @param i x
* @param j y
*/
public boolean findWay(int i, int j) {
//假设[6, 5]为终点,到达终点,跳出递归
if (maze[6][5] == 2) {
System.out.println("**** 成功找到终点! *****");
viewMaze(); //查看迷宫
return true;
}
//判断坐标是否可以行走
if(maze[i][j] == 0) {
//可以走,先将当前位置设置已走(2)
maze[i][j] = 2;
//再尝试向下走
if (findWay(i+1, j)) {
//接收到true返回值(找到终点),才跳出递归,下面类似
return true;
}
//向下走不通,尝试向右走
if (findWay(i, j+1)) {
return true;
}
//向下,向右走不通,尝试向上走
if (findWay(i-1, j)) {
return true;
}
//向下,向右,向上走不通,尝试向左走
if (findWay(i, j-1)) {
return true;
}
//若都走不通,设置为3,禁止向这格方法行走
maze[i][j] = 3;
return false;
}else {
//不能走,返回false
return false;
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
9
public void mazeTest() {
//创建迷宫,并查看迷宫
Maze maze = new Maze();
maze.viewMaze();
//从[1, 1]找路
maze.findWay(1, 1);
}

3 应用:八皇后问题
3.1 问题

3.2 代码
- (1)思路
- 从第一行第一个开始遍历,成功放了一个就往下一行继续从0号位遍历,直到不冲突,就继续遍历下一行
- 可以用八个for循环来解决,但是代码会十分的难看,且不易看懂
- 而用递归的形式,代码变得分成简洁
- (2)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69public class Queen8 {
int max = 8; //皇后数量,默认为8
int count = 1; //统计方法种数
int[] locations; //八皇后位置,以一维数组表示位置,index代表'行数',index对应的数据代表'列数'
public Queen8() {
locations = new int[max];
}
/**
* 计算八皇后问题
* @param row 行号
*/
public void getLocation(int row) {
//行号 === 行长度,位置计算完毕,打印并退出递归
if (row == max) {
print();
return;
}
//遍历位置
for (int location=0; location<max; location++) {
locations[row] = location;
//判断位置是否冲突
if(!isConflict(row)) {
//没有冲突,递归下一行
getLocation(row+1);
}
}
}
/**
* 判断是否冲突
* @param row 行号
* @return boolean
*/
public boolean isConflict(int row) {
//循环遍历每行
for(int i=0; i<row; i++) {
//当处于同一列,或同一条斜线(斜率为1,也理解为等腰直角三角形)
if (locations[i] == locations[row]
|| row-i == Math.abs(locations[row] - locations[i])) {
return true;
}
}
return false;
}
/**
* 打印结果
*/
private void print() {
if (count < 10) {
System.out.printf("第0%d种:", count);
}else {
System.out.printf("第%d种:", count);
}
count++;
for (int location : locations) {
System.out.printf("%d\t", location);
}
System.out.println();
}
}
- (3)测试
1
2
3
4
5
public void queen8Test() {
Queen8 queen8 = new Queen8();
queen8.getLocation(0);
}