排序算法,是算法基础入门,下面介绍八种的排序算法的实现
1 排序算法
1.1 介绍
- 排序,也称为排序算法(Sort Algorithm),排序一组数据,依指定的顺序进行排序的过程
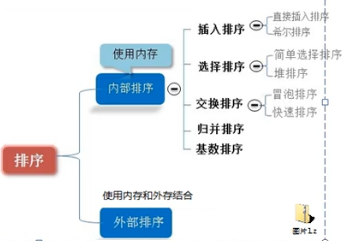
- 排序分类:
- (1)内部排序:将需要处理的所有数据都加载到内部存储器中进行排序
- (2)外部排序:数据量过大,无法全部加载到内存中,需要借助外部存储进行排序
2 冒泡排序
2.1 介绍
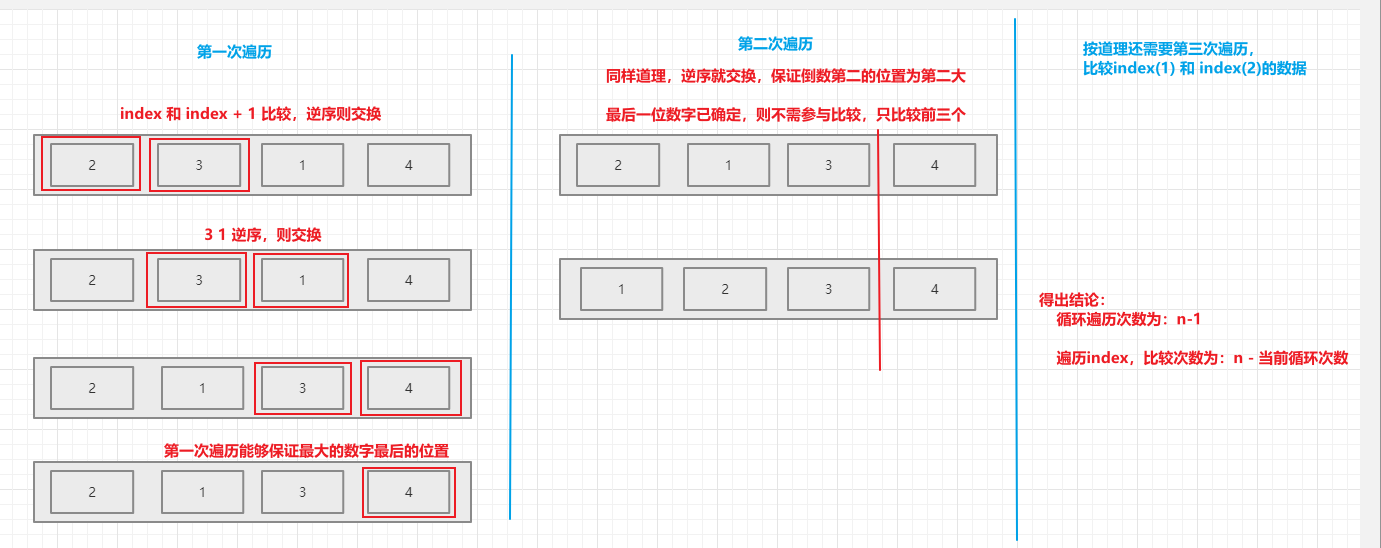
- 冒泡排序(Bubble Sorting) 的基本思想为:通过遍历比较序列,依次比较当前index,和index+1是否逆序,逆序则交换两者位置,最后变成最小 / 最大的放在末尾位置,后续遍历依次放倒数第二,倒数第三…等位置,以此类推,遍历结束则为有序序列。就仿佛水底下的气泡逐渐上升
- 时间复杂度:O(n^2)
- 算法优化:如果一趟遍历下没有进行过任何交互,证明序列为有序,就直接停止循环遍历。可以设置一个变量来记录一次遍历中是出现交换
2.2 图解算法
2.3 代码
- (1)基础代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25public class BubbleSort {
/**
* 升序排序
* @param arr 排序序列
*/
public static void asc(int[] arr){
int n = arr.length; //数组长度
int temp; //中间变量
//遍历次数为:长度-1 次
for(int i=0; i<n-1; i++) {
//比较次数为:n-当前遍历次数(因为i从0开始,要额外-1,即n-(i+1))
for (int j=0; j<n-i-1; j++) {
if (arr[j] > arr[j+1]) {
//利用中间变量交换位置
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
public void bubbleSortTest() {
//创建数组,并调用方法排序
int[] arr = new int[]{2, 1, 5, -2};
BubbleSort.asc(arr);
for (int item : arr) {
System.out.printf("%d ", item);
}
}
2.4 优化代码
- 在上面基础代码上添加一个变量记录是否发生交换,未发生交换,序列为有序,方法退出
1 | /** |
3 选择排序
3.1 介绍
- 选择排序(select sorting):属于内部排序法,从欲排序的数据中,按照指定的规则选择出来摸一个元素,在依规定交换位置后大大排序的目的
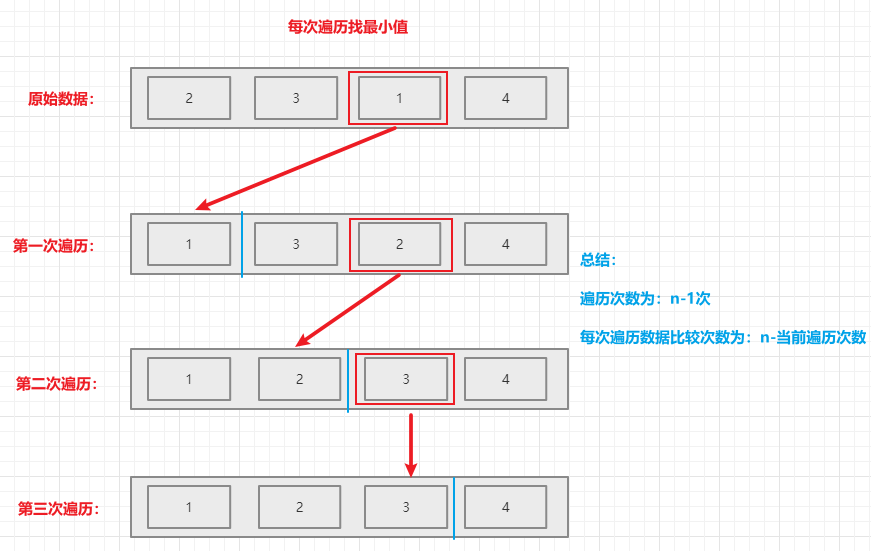
- 算法思路:遍历数据,选出最小 / 最大的数据,将其交换防止数组开启;后续的遍历类型,选出最小 / 最大 放在后一位
- 与冒泡区别:判断的次数几乎一样,但数据之间的交换次数变少,速度比冒泡快
- 算法优化:如果当前起始位置刚好就是最小值,则无需交换,添加一个if判断来处理
3.2 图解算法
3.3 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34public class SelectSort {
/**
* 选择排序 - 升序
* @param arr 排序序列
*/
public static void asc(int[] arr) {
int n = arr.length; //数组大小
int temp; //中间变量:存储最小值
int index; //记录最小值的下标
//遍历次数:n-1次
for(int i=0; i<n-1; i++) {
//遍历数据,起始位置为当前遍历次数-1(即 i)
//默认将起始位置(i)数据作为最小值
temp = arr[i];
index = i;
//因为i默认为最小值,无需跟自己比,j从i+1开始比较
for(int j=i+1; j<n; j++) {
//发现更小的值,则记录其值和下标
if (arr[j] < temp) {
temp = arr[j];
index = j;
}
}
//找完最小值,利用中间变量交换数据
arr[index] = arr[i];
arr[i] = temp;
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
public void selectSortTest() {
//创建数据并排序
int[] arr = new int[]{2, 1, 5, -2};
SelectSort.asc(arr);
System.out.println(Arrays.toString(arr));
}
3.4 代码优化
- 添加一个判断,如果当前起始位置就是最小值,则无需进行交换
1 | /** |
4 插入排序
4.1 介绍
- 插入排序(insert sorting):属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,已达到排序目的
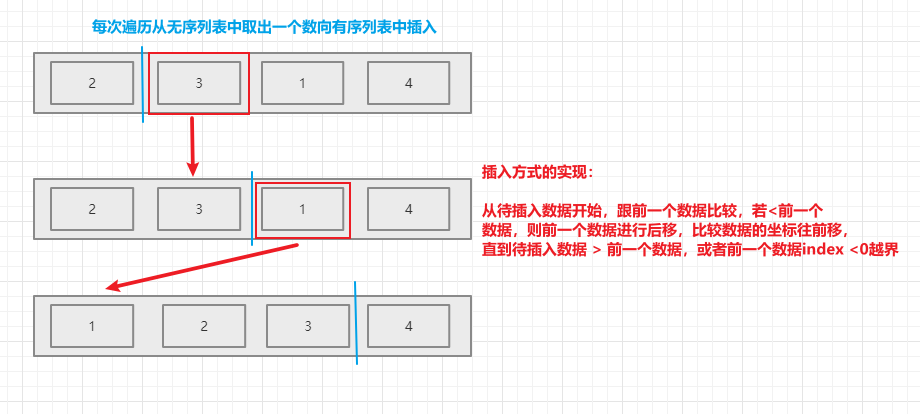
- 算法思路:把n个待排序的元素分为有序表和无序表,每次遍历从无序表中,取出一个元素,跟有序表中的数据进行比较,找到合适的位置,进行插入
- 插入方法:待插入数据跟前一个数据比较大小,大小顺序不对,则前一个数据进行后移,再跟前前一个数据比较,直到大小顺序合适 或 已经没有前一个数据
- 跟冒泡比较:看起来和冒泡相似,一个将数据往后移,一个将数据往前移;但是插入排序只是将数据后移,并没有交换两者之间的数据,操作步骤对比冒泡是少了一步,算法速度更快
4.2 算法图解
4.3 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22public class InsertSort {
/**
* 插入排序 - 升序
* @param arr 序列
*/
public static void asc(int[] nums) {
// i表示当前要插入的数据
for (int i=1; i<nums.length; i++) {
int idx = i;
int temp = nums[i];
// i开始,从后往前比较,插入数小于前数,则前数后移
while (idx > 0 && temp < nums[idx-1]) {
nums[idx] = nums[idx-1];
idx --;
}
// idx发生变化,数据发生后移,则插入数据
if (idx != i) {
nums[idx] = temp;
}
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
public void insertSortTest() {
//创建数据并排序
int[] arr = new int[]{2, 1, 5, -2};
InsertSort.asc(arr);
System.out.println(Arrays.toString(arr));
}
5 希尔排序
5.1 介绍
- 希尔排序(shell sorting):该算法由希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后一个更高效的版本,也称为缩小增量排序
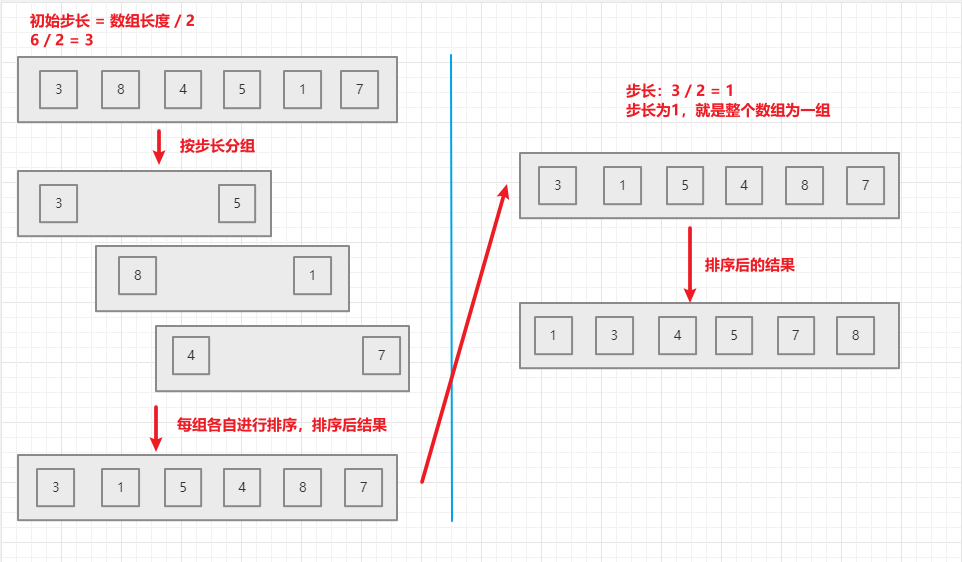
- 算法思想:对序列按指定步长进行分组,对每个组执行一次排序算法。然后不断缩小分组,最后合成一个组,执行排序算法,形成有序序列
- 优点:将数据缩小进行排序,速度快之余,并将避免很小的数在最后,需要一步一步往前挪的情况,算法运行的时间比其他算法相对于稳定
5.2 算法图解
5.3 希尔排序-交换法(不推荐)
- 代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26/**
* 希尔排序-交换法(冒泡排序)-升序
* @param arr 待排序队列
*/
public static void ascBySwitch(int[] arr) {
int n = arr.length; //数组长度
int temp; //中间变量(用于交换)
int step = n/2; //步长
//因为步长为1时,再计算步长1/2=0,会退出循环
//前两个循环用于分组
while(step > 0) {
for (int i=step; i<n; i++) {
//类似冒泡排序,只不过是从后往前按照指定步长比较(效率慢)
for (int j=i-step; j>=0; j-=step) {
if (arr[j] > arr[j+step]) {
temp = arr[j];
arr[j] = arr[j+step];
arr[j+step] = temp;
}
}
}
//修改步长
step = step / 2;
}
}
5.4 希尔排序-移位法(推荐)
- 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33/**
* 希尔排序-移位法(插入排序)-升序
* @param arr 待排序队列
*/
public static void ascByMove(int[] arr) {
int n = arr.length; //队列长度
int step = n/2; //步长
int temp; //记录待插入数据
int index; //记录待插入数据的下标
//前两个循环用于分组
while (step > 0) {
for (int i=step; i<n; i++) {
//记录待插入数据
temp = arr[i];
index = i;
while(index-step>=0 && temp<arr[index-step]) {
//数据后移
arr[index] = arr[index - step];
index -= step;
}
//数据位置发生移动,才插入数据
if (index != i) {
arr[index] = temp;
}
}
//修改步长
step /= 2;
}
}
6 快速排序
6.1 介绍
- 快速排序(QuickSort):是对冒泡排序的一种改进
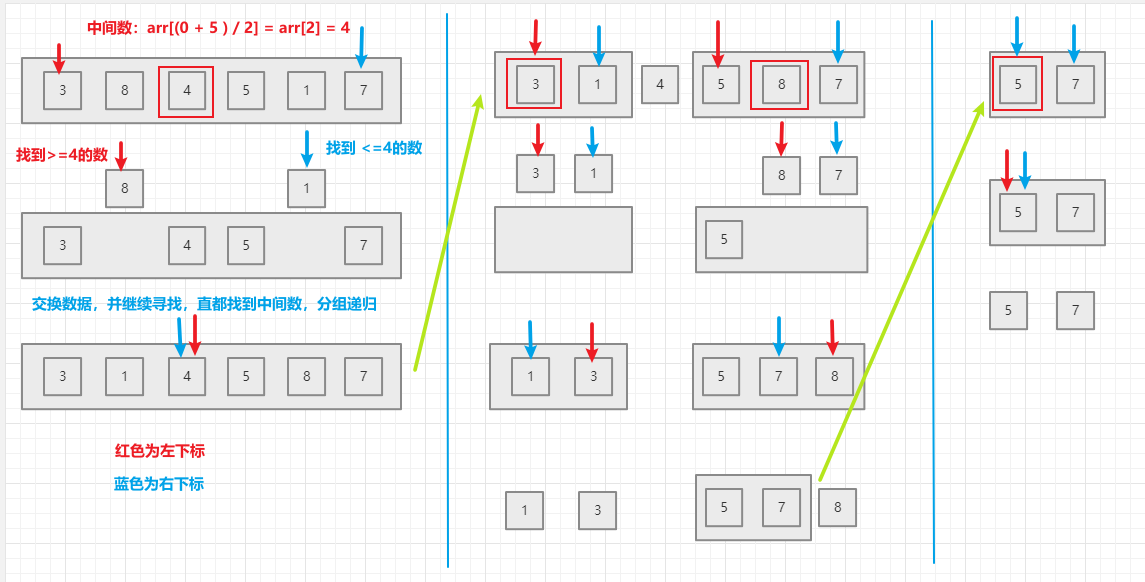
- 算法思想:选定一个数据作为边界,通过一趟排序将要排序的数据分为两部分,一边小于选定的数据,另一边大于选定的数据。然后对此两组数据,按照上面方法再进行分组。一直递归执行,直到分组的数据小于等于1个时,才退出递归
- 优点:利用空间来换取时间的典型案例,利用递归来排序,速度快。但因为使用了递归,当数据量庞大的时候,会出现栈溢出的情况(递归本身是使用了栈)
6.2 图解
6.3 代码实现
1 | public void quickSort(int[] nums) { |
7 归并排序
7.1 介绍
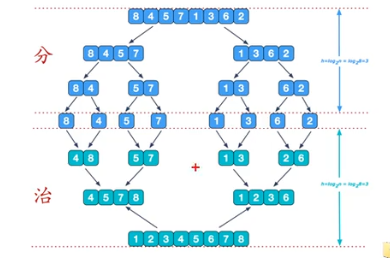
- 归并排序(Merge Sort):利用归并的思想实现的排序算法,采用经典的分治策略(分:将问题分成一个小的问题然后递归求解;治:将分的阶段得到的答案结合在一起)
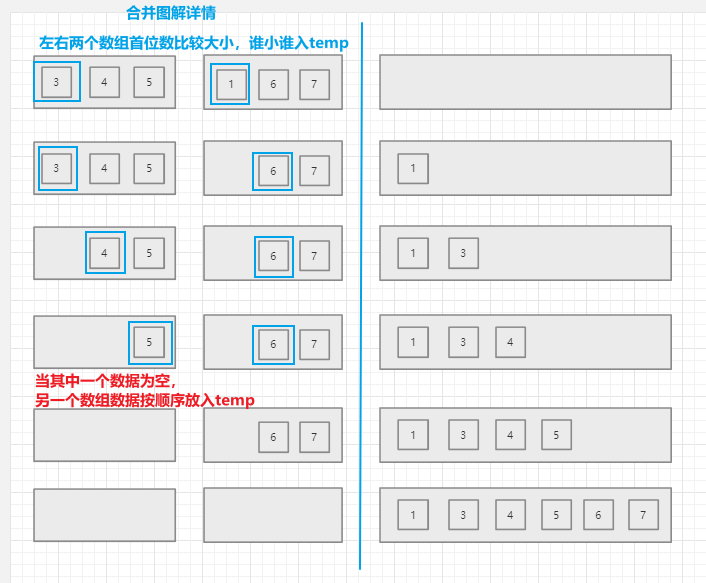
- 算法思路:将数组的数组递归细分,分到只为1时。再对两个数组按大小顺序加入到一个缓存数组temp,再将缓存数组temp的数据改写进原数组数据
- 优点:和快速排序一样,引入了递归,牺牲空间来换取时间
7.2 图解
7.3 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84public class MergeSort {
/**
* 归并排序 - 升序
* @param arr 待排序数组
*/
public static void asc(int[] arr) {
divideConquer(arr, 0, arr.length-1);
}
/**
* '分 + 治' : 将数组递归分割,并按顺序合并
* @param arr 待排序原数组
* @param left 左边界下标
* @param right 右边界下标
*/
private static void divideConquer(int[] arr, int left, int right) {
int mid = (left + right) / 2;
//当左右边界不重合,可以继续分
if (left < right) {
//对左右两边继续进行分
divideConquer(arr, left, mid);
divideConquer(arr, mid+1, right);
//分完再进行'治'
conquer(arr, left, mid, right);
}
}
/**
* '治':将两数组比较按顺序加入暂时变量,并改写原数组
* @param arr 待排序序列
* @param left 左边界下标
* @param mid 中间下标(用于将一个数组分割为两个数组)
* @param right 右边界下标
*/
private static void conquer(int[] arr, int left, int mid, int right) {
int lIndex = left; //左边数组头下标
int rIndex = mid + 1; //右边数组头下标
int[] temp = new int[right - left + 1]; //暂时变量
int tIndex = 0; //temp数组下标
//只要下标没有移动到尾部,一直比较两数组大小
while(lIndex <= mid && rIndex <= right) {
//比较两个数组的头下标的大小,谁小谁加入temp
if (arr[lIndex] < arr[rIndex]) {
temp[tIndex] = arr[lIndex];
tIndex ++;
lIndex ++;
}else {
temp[tIndex] = arr[rIndex];
tIndex ++;
rIndex ++;
}
}
//将剩余数据加入到temp数组
//左边数组有剩
while (lIndex <= mid) {
temp[tIndex] = arr[lIndex];
tIndex ++;
lIndex ++;
}
//右边数组有剩
while (rIndex <= right) {
temp[tIndex] = arr[rIndex];
tIndex ++;
rIndex ++;
}
//改写arr数组数据
tIndex = 0;
for (int i=left; i <= right; i++) {
arr[i] = temp[tIndex];
tIndex ++;
}
}
}
- (2)测试代码
1
2
3
4
5
6
7
8
public void mergeSortTest() {
int[] arr = new int[]{8, 4, 5, 7, 1, 3, 6, 2};
MergeSort.asc(arr);
System.out.println(Arrays.toString(arr));
}
8 基数排序
8.1 介绍
- 基数排序(Radix Sort):属于“分配式排序(Distribution Sort)”,又称为“桶子排序(bucket Sort)”。顾名思义,它通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的效果
- 基数排序是属于稳定性的排序,基数排序是效率高的稳定性排序法
- 基数排序是桶排序的拓展
- 实现方法,将整数按位数切割成不同的数字,然后按每个位数分别比较
- 算法思路:创建10个桶(负数19个),分别代表0, 1, 2, 3, 4, 5, 6, 7, 8, 9,对数组数据求个位数,将数据放入对应个位数的桶中,遍历完毕后按照顺序取出桶中数据放回数组中。下次就取十位数,下下次取百位数,以此类推,直到达到数据中最大位数为止
8.2 图解

8.3 代码
- 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53public class RadixSort {
/**
* 基数排序 - 升序
* @param arr 待排序序列
*/
public static void asc(int[] arr) {
int n = arr.length; //数组长度
int index; //数组下标
int[][] buckets = new int[19][n]; //定义桶(算上负数19个桶)
int[] count = new int[19]; //记录桶中数据个数
int digit = 1; //位数倍数:个位数1,十位数10,百位数100,以次类推
int temp; //暂时变量
//遍历数组求出最大位数
int max = 0;
for (int data : arr) {
//将数据取绝对值,转为字符串,求长度可得位数
int length = String.valueOf(Math.abs(data)).length();
if (length > max) {
max = length;
}
}
int times = 0; //记录循环次数
while (times < max) {
//遍历数组存放数据
for (int data : arr) {
temp = data / digit % 10; //求位数
buckets[temp + 9][count[temp + 9]] = data; // +9为了跳过负数的9个桶,-9+9=0就放在0号位桶
count[temp + 9] ++; //桶中数据个数 + 1
}
//取出桶中数据放入原数组
index = 0;
for (int i=0; i<buckets.length; i++) {
//桶中数据不为0,取出数据覆盖原数组
if (count[i] > 0) {
for (int j=0; j<count[i]; j++) {
arr[index] = buckets[i][j];
index ++;
}
count[i] = 0; //数据个数清0
}
}
digit *= 10; //修改位数倍数
times ++; //次数+1
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
public void radixSortTest() {
int[] arr = new int[]{132, 125, 43, -51, -72, -115};
RadixSort.asc(arr);
System.out.println(Arrays.toString(arr));
}
9 堆排序
9.1 介绍
- 前提:堆排序的使用时需要数据结构-树的基础知识建议学完树形结构再来学习堆排序
- 堆:是具有一定性质的完全二叉树。
- (1)每个节点的值都大于或等于其左右孩子节点的值,称为大顶堆
- (2)每个节点的值都小于或等于其左右孩子节点的值,称为小顶堆
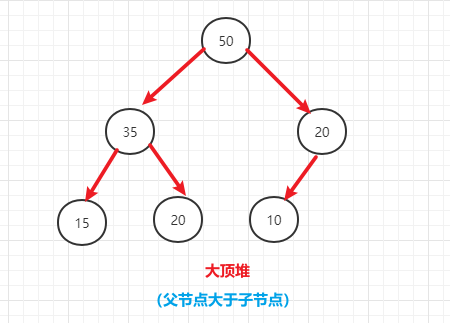
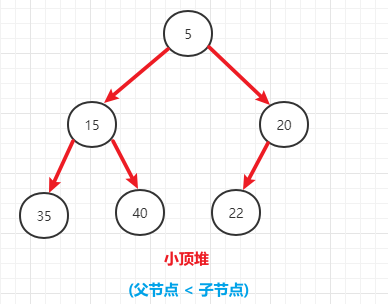
- 堆排序:利用堆来设计的一种排序算法,堆排序是一种选择排序(逐步选择最大/最小值进行处理)。最坏、最好、平均时间复杂度为
O(nlogn),属于不稳定排序。升序使用大顶堆,降序使用小顶堆
9.2 思路
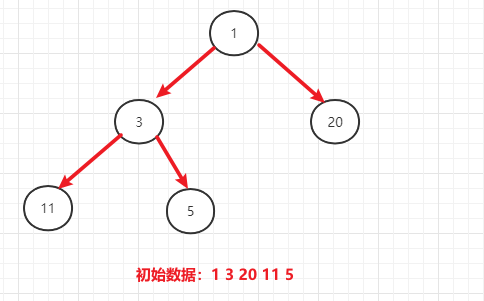
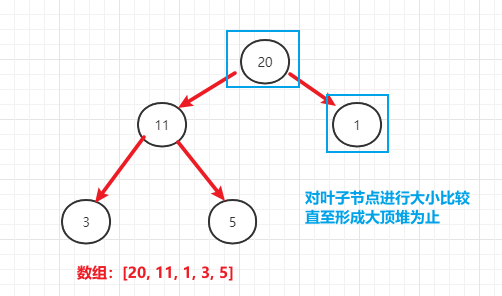
- (1)将待排序的序列构建成一个大顶堆(顺序存储二叉树)
- 形成大顶堆规则:
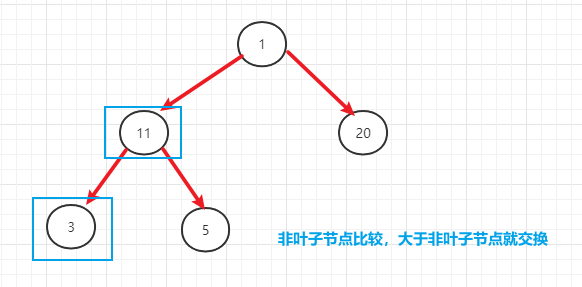
- 1、父节点跟子节点比较时从最后的父节点开始比较,逐步往前移
- 2、如果父节点与子节点发生交换后,判断交换后的子节点是否是父节点,如果是父节点,还要继续跟其子节点进行判断(因为会出现从顶部换一个很小的数给其子节点,而该子节点也是一个父节点,导致父节点<子节点)
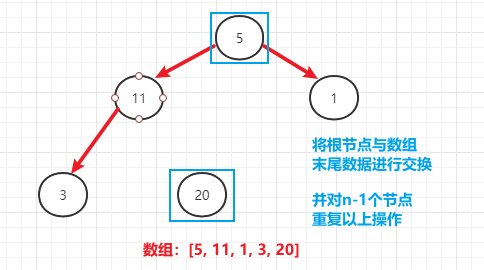
- (2)形成大顶堆后,顶部的根节点就是一个数组的最大值,将其与末尾元素进行交换,此时最大值已经确定了
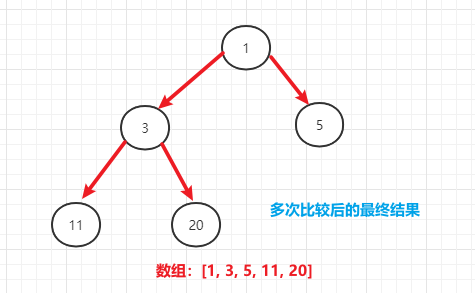
- (3)对剩余的n-1个树重复上面操作(构建大顶堆,交换最大值)
9.3 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62public class HeapSort {
/**
* 堆排序 - 升序
* @param arr 待排序数组
*/
public static void asc(int[] arr) {
int arrLength = arr.length; //数组长度
int temp; //中间变量
//当数组比较个数 <= 1结束循环
while (arrLength > 1) {
//从最后一个父节点往前遍历(最后一个父节点为 n/2-1,前面的节点都是父节点)
for(int i = arrLength/2-1; i >= 0; i --) {
//实现父节点 > 子节点
toLargeTop(arr, i, arrLength);
}
//形成大顶堆后,根节点和数组末尾交换数据
temp = arr[arrLength-1];
arr[arrLength-1] = arr[0];
arr[0] = temp;
//数组长度减一,排除最后已确定的数据
arrLength--;
}
}
/**
* 从上到下实现 父节点 > 子节点
* @param arr 待排序数组
* @param parentIndex 父节点下标
* @param arrLength 数组长度
*/
public static void toLargeTop(int[] arr, int parentIndex, int arrLength) {
int temp; //记录父节点大小
int childIndex = parentIndex * 2 + 1; //计算左子节点下标
while (childIndex < arrLength) {
temp = arr[parentIndex];
//存在右子节点 且 右子节点>左子节点
if (childIndex + 1 < arrLength && arr[childIndex] < arr[childIndex + 1]) {
childIndex++;
}
//比较子节点与父节点大小
if (arr[childIndex] > arr[parentIndex]) {
arr[parentIndex] = arr[childIndex];
arr[childIndex] = temp;
parentIndex = childIndex; //发生交换,父节点下标往下移,比较后面的子节点是否也要发生变化
}else {
//没发生交换就退出循环
break;
}
//重新计算子节点下标
childIndex = parentIndex * 2 + 1;
}
}
}
- (2)测试
1
2
3
4
5
6
7
public void heapSortTest() {
int[] arr = new int[]{1, 3, 20 ,11, 5};
HeapSort.asc(arr);
System.out.println(Arrays.toString(arr));
}