查找算法的介绍和代码实现
1 线性查找
1.1 介绍
- 线性查找(Linear Search):也称为顺序查找,顾明思义,就是按顺序遍历序列,找到对应匹配的数据,返回该数据所在的下标
1.2 代码
- 由于线性查找过于简单,就不多做思想说明
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38public class LinearSearch {
/**
* 线性查找 - 查找一个
* @param arr 查找数组
* @param key 查找值
* @return int
*/
public static int findOne(int[] arr, int key) {
//遍历数组,比较数据
for(int i=0; i<arr.length; i++) {
if (arr[i] == key) {
return i;
}
}
//没有找到返回-1
return -1;
}
/**
* 线性查找 - 查找全部
* @param arr 查找数组
* @param key 查找值
* @return List<Integer>
*/
public static List<Integer> findAll(int[] arr, int key) {
List<Integer> temp = new ArrayList<>();
//遍历数组,比较数据
for(int i=0; i<arr.length; i++) {
if (arr[i] == key) {
temp.add(i);
}
}
return temp;
}
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
11
12
public void linearSearchTest() {
int[] arr = new int[]{1, -2, 5, 11, 190, 11, -45, -2};
//查找一个
int index = LinearSearch.findOne(arr, 11);
System.out.println("数字11的下标为:" + index);
//查找全部
List<Integer> indexList = LinearSearch.findAll(arr, 11);
System.out.println("数字11的下标分别为:" + indexList.toString());
}
2 二分查找
2.1 介绍
- 二分查找(Binary Search):即将一个有序的数组分为左右两部分,将查找值和中间值比较,根据大小来选取左右哪一部分在进行下一次查找,来缩小查找的范围
- 算法思路:通过
mid = (left + right) / 2或mid = left + 1/2 (right - left)取出中间下标,对数组分为左右两部分,通过中见下标取出对应中间值。通过查找值key与中间值比较,大于中间值,就选取右边的部分[mid+1, right]进行递归查找,反之对左边[left, mid-1]进行递归查找。递归退出条件:(1)查到对应的值arr[mid] == key;(2)找不到对应的值,即超出边界left > rigth
2.2 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48public class BinarySearch {
/**
* 二分查找 - 升序数组 - 查找一个
* @param arr 查找数组
* @param key 查找值
* @return int
*/
public static int findOneByAsc(int[] arr, int key) {
//因为是有序数组,超出边界值一定不存在,直接退出
if (key < arr[0] || key > arr[arr.length-1]) {
return -1;
}
return findOneRecursion(arr, 0, arr.length-1, key);
}
/**
* 查找一个 - 递归查找
* @param arr 查找数组
* @param left 左边界下标
* @param right 右边界下标
* @param key 查找值
* @return int
*/
private static int findOneRecursion(int[] arr, int left, int right, int key) {
//超出边界,找不到相应的值
if (left > right) {
return -1;
}
int mid = (left + right) / 2; //中间下标
//值相等,找到下标
if (arr[mid] == key) {
return mid;
}
//值 > key,向左边部分递归查找
else if (arr[mid] > key) {
return findOneRecursion(arr, left, mid - 1, key);
}
//值 < key,向右边部分递归查找
else {
return findOneRecursion(arr, mid + 1, right, key);
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
public void binarySearch() {
int[] arr = new int[]{1, 4, 7, 11, 11, 34, 111};
//查找一个
int index = BinarySearch.findOneByAsc(arr, 11);
System.out.println("数字11的下标为:" + index);
}
2.3 非递归写法
(1)代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37/**
* 二分查找算法 - 非递归
* @author letere
* @create 2021-06-05 15:31
*/
public class BinarySearch2 {
/**
* 二分查找 - 升序序列 - 查找一个
* @param arr 升序序列
* @param key 查找值
* @return int
*/
public static int findOneByAsc(int[] arr, int key) {
int left = 0;
int right = arr.length-1;
int mid;
while (left <= right) {
mid = (right + left) / 2;
//中间值匹配,返回下标
if (arr[mid] == key) {
return mid;
}
//中间值 < 查找值,向右查找,反之向左查找
if (arr[mid] < key) {
left = mid + 1;
}else {
right = mid - 1;
}
}
return -1;
}
}(2)测试
1
2
3
4
5
6
7
8
public void binarySearch() {
int[] arr = new int[]{1, 4, 7, 11, 11, 34, 111};
//查找一个
int index = BinarySearch2.findOneByAsc(arr, 11);
System.out.println("数字11的下标为:" + index);
}
2.4 功能完善
- 如果我们需要查找所有的下标值,我么可以对上面的代码进行改进:在找到对应的下标后,先不着急返回,而是遍历该下标左右两边的值。因为是一个有序数组,相同值就会在其左右两边附近。如果值等于查找值,也将其加入返回值中。最后再统一返回
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62/**
* 二分查找 -升序数组 - 查找全部
* @param arr 查找数组
* @param key 查找值
* @return List<String>
*/
public static List<Integer> findAllByAsc(int[] arr, int key) {
//因为是有序数组,超出边界值一定不存在,直接退出
if(key < arr[0] || key > arr[arr.length-1]) {
return new ArrayList<>();
}
return findAllRecursion(arr, 0, arr.length-1, key);
}
/**
* 查找全部 - 递归查找
* @param arr 查找数组
* @param left 左边界下标
* @param right 右边界下包
* @param key 查找值
* @return List<String>
*/
private static List<Integer> findAllRecursion(int[] arr, int left, int right, int key) {
//超出边界,查找失败
if (left > right) {
return new ArrayList<>();
}
int mid = (left + right) / 2;
//值相等,找到下标
if(arr[mid] == key) {
List<Integer> indexList = new ArrayList<>(); //下标集合
indexList.add(mid);
//向左找同样值的下标
int temp = mid -1; //暂时变量,记录下标
while (temp >= 0 && arr[temp] == key) {
indexList.add(temp);
temp --;
}
//向右找同样值的下标
temp = mid + 1;
while (temp < arr.length && arr[temp] == key) {
indexList.add(temp);
temp ++;
}
return indexList;
}
//值 > key,向左边部分递归寻找
else if(arr[mid] > key) {
return findAllRecursion(arr, left, mid-1, key);
}
//值 < key,向右边部分递归寻找
else {
return findAllRecursion(arr, mid+1, right, key);
}
}
- (2)测试
1
2
3
4
5
6
7
8
public void binarySearch() {
int[] arr = new int[]{1, 4, 7, 11, 11, 34, 111};
//查找全部
List<Integer> indexList = BinarySearch.findAllByAsc(arr, 11);
System.out.println("数组11的下标分别为:" + indexList.toString());
}
3 插值查找
3.1 介绍
- 插值查找(Interpolation Search):是二分查找的拓展查找。每次分左右两个数组,不再是中间的下标。而是一个自适应的下标,根据数组和查找值变化。插值算法在一些分布比较均匀,以及等差序列的时候,算法效率很高。
- 算法思想:整体和二分查找一样。唯一区别就是数组的分界下标不再是中间值,而是
left + (key - arr[left]) / (arr[right] - arr[left]) * (right - left),其中的(key - arr[left]) / (arr[right] - arr[left])是计算该查找值在整个数组中的占比,来大概估算其对应的下标。二分查找这里的值直接为1/2。
3.2 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48public class InterpolationSearch {
/**
* 插值查找 - 升序数组 - 查找一个
* @param arr 查找数组
* @param key 查找值
* @return int
*/
public static int findOneByAsc(int[] arr, int key) {
//因为是有序数组,如果查找值超出边界,肯定查找不到
if (key < arr[0] || key > arr[arr.length-1]) {
return -1;
}
return findOneRecursion(arr, 0, arr.length-1, key);
}
/**
* 查找一个 - 递归查找
* @param arr 查找数组
* @param left 左边界下标
* @param right 右边界下标
* @param key 查找值
* @return int
*/
private static int findOneRecursion(int[] arr, int left, int right, int key) {
//超出边界,查找不到
if(left > right) {
return -1;
}
//计算查找值在该数组的占比下标
int rate = left + (key - arr[left]) / (arr[right] - arr[left]) * (right - left);
//找到相应值,返回下标,退出递归
if (arr[rate] == key) {
return rate;
}
//值 > key,向左边部分递归查找
else if (arr[rate] > key) {
return findOneRecursion(arr, left, rate-1, key);
}
//值 < key,向右边部分递归查找
else {
return findOneRecursion(arr, rate+1, right, key);
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
public void interpolationSearchTest() {
int[] arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
//查找一个
int index = InterpolationSearch.findOneByAsc(arr, 1);
System.out.println("数字1的下标为:" + index);
}
4 斐波那契查找
4.1 介绍
- 黄金分割点:一条线段分割为两部分,这两部分之间比值约等于
0.618,就称为该切割点为黄金切割点
- 斐波那契数列:{1, 1, 2, 3, 5, 8, 13, 21, 34, 55….},即后面数字时前两个数字之和,可以返现相邻两个数的比例,无限接近黄金分割值
0.618,例:34 / 55
- 斐波那契查找(Fibonacci Search):又称为黄金分割法,利用斐波那契数列接近黄金分割值的特点,对一个数组,求出其长度。找出最接近的斐波那契数列值(数组长度不够就扩容),该值的前两个值,就是对数组分割后左右两边的长度。
4.2 思路详解
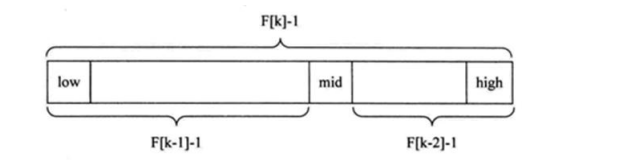
- (1)找分割点原理
- 按照斐波那契数列的特点:
F[k] = F[k-1] + F[k-2],后面的数 = 前两个数之和 - 可以推导出
F[k]-1 = F[k-1]-1 + F[k-2]-1 + 1 - 按照上面公式可以理解为:对于长度为
F[k]-1的数组,可以切割成左边长度为F[k-1]-1和右边长度为F[k-2]-1长度的数组,多出来的1就是中间的黄金分割点 - 也因此可以得到黄金分割点 =
low + F[k-1]-1
- (2)递归/循环查找数据原理
- 跟二分法一样,比较查找值与黄金分割点值,判断该数据的左右位置
- 如果查找值在左边,修改
右边界index = 分割点index - 1,并修改记录的数组长度,因为原长度为F[k]-1,变成了F[k-1]-1,所以我们只需要修改k值,k=k-1即可 - 查找值在右边跟左边大致同理,修改
左边界index = 分割点index + 1,和k=k-2 - 递归 / 循环重新计算分割值黄金分割点即可
4.3 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79public class FibonacciSearch {
/**
* 获取斐波那契数组
* @return int[]
*/
private static int[] getFibArray() {
int n = 20; //默认数组长度20,按需修改
int[] fibArray = new int[n];
//填写斐波那契数列数据
fibArray[0] = 1;
fibArray[1] = 1;
for(int i=2; i<n; i++) {
fibArray[i] = fibArray[i-1] + fibArray[i-2];
}
return fibArray;
}
/**
* 斐波那契查找 - 升序数组 - 查找一个(循环)
* @param arr 查找数组
* @param key 查找值
* @return int
*/
public static int findOneByAsc(int[] arr, int key) {
int n = arr.length; //数组长度
int left = 0; //左边界下标
int right = n - 1; //右边界下标
int goldenIndex = 0; //黄金分割点
int fibIndex = 0; //斐波那契数列下标
//获取斐波那契数列
int[] fibArray = getFibArray();
//确定fibIndex值,F(k)-1大于/等于数组长度
while (n > fibArray[fibIndex] - 1) {
fibIndex ++;
}
//对原数组进行扩容,使其传长度等于fibArray[fibIndex]-1
int[] temp = Arrays.copyOf(arr, fibArray[fibIndex]-1);
//对多出的0数据填补为末尾的数据
for (int i=right; i<temp.length; i++) {
temp[i] = arr[right];
}
while (left <= right) {
//计算黄金分割点
goldenIndex = left + fibArray[fibIndex-1] - 1;
//值 < 分割点值,数据在分割点的左边
if (key < temp[goldenIndex]) {
right = goldenIndex - 1; //修改右边界
fibIndex --; //斐波那契值往前移1位:F[k] = F[k-1] + F[k-2],左边部分的长度 = F[k-1]
}
//值 > 分割点值,数据在分割点的右边
if (key > temp[goldenIndex]) {
left = goldenIndex + 1; //修改左边界
fibIndex -= 2; //F[k] = F[k-1] + F[k-2],右边部分长度 = F[k-2]
}
//值 = 分割点值,找到数据
if (key == temp[goldenIndex]) {
//判断分割点值是否在扩容位置,在就返回原数组末尾下标
if (goldenIndex > n-1) {
return n-1;
}
return goldenIndex;
}
}
return -1;
}
}
- (2)测试
1
2
3
4
5
6
7
public void fibonacciSearch() {
int[] arr = new int[]{1, 4, 7, 11, 15, 34, 111};
int index = FibonacciSearch.findOneByAsc(arr, 11);
System.out.println("数字11的下标为:" + index);
}