数据结构:数的介绍和基本实现代码
1 树
1.1 存储方式比较
- (1)数组
- 优点:通过下标方式访问元素,速度快。对于有序数组,还可以使用二分查找提高检索速度
- 缺点:如果要检索某个具体的值,或者插入值会进行整体移动,效率低
- (2)链表
- 优点:在一定程度上对数组进行优化,对插入、删除操作进行优化,只需修改结点间的指向即可,无需整体移动
- 缺点:链表进行检索,效率很低
- (3)树
- 能提高数据存储、读取效率,比如利用二叉排序树,既可以保证数据的检索数据,同时也能保证数据的插入和删除的速度
1.2 树的常用术语
- (1)节点:一个对象,用来存储数据,跟链表类似
- (2)根节点:一树最顶部的节点
- (3)父/子节点:节点A的下一个节点指向节点B,A就是B的父节点,B是A的子节点
- (4)叶子节点:没有子节点的节点,即树的最底部节点
- (5)节点的权:理解为节点数据的大小(大小可根据一定条件/公式计算)
- (6)路径:从根节点到指定节点的路线(即:经过了哪些节点)
- (7)子树:一个树里包含另一个树,被包含的树称为子树
- (8)树的高度:树的层数(行数)
- (9)森林:多棵子树构成为森林
2 二叉树
2.1 介绍
- 二叉树:顾名思义,二叉树即一个节点只有两个子节点(左节点和右节点)的树,为二叉树
- 满二叉树:如果二叉树的所有叶子节点都在最后一层,即节点数为
2^n-1(n = 层数)的树为满二叉树

- 完全二叉树:二叉树所有叶子节点在最后一层或两层,且这两层之间的节点是连续的,没有断开,称为完全二叉树

2.2 前中后序遍历

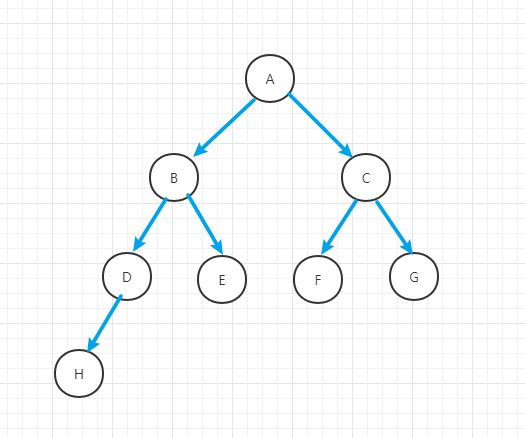
- (1)前序遍历:先输出父节点,再遍历左子树,然后右子树(子树也有自己对应的父节点,所以会一直遍历左边,然后才到右边)
- 上图:A -> B -> D -> H -> E -> C -> F -> G
- (2)中序遍历:先遍历左子树,再输出父节点,然后再遍历右子树
- 上图:H -> D -> B -> E -> A -> F -> C -> G
- (3)后序遍历:先遍历左子树,再遍历右子树,最后输出父节点
- 上图:H -> D -> E -> B -> F -> G -> C -> A
2.3 遍历代码实现
- (1)代码实现(递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128public class BinaryTree {
//子类:节点
private class Node {
public int rate; //权重
public Object data; //数据
public Node left; //左子节点
public Node right; //右子节点
public Node(int rate, Object data) {
this.rate = rate;
this.data = data;
}
public String toString() {
return "Node{" + rate + ": " + data + '}';
}
}
//-----------------------------------------------------
private Node root; //根节点
public BinaryTree() {
//因为最基础的二叉树没有任何规则,所以不适合自动创建,需要我们手动创建二叉树
root = new Node(1, "hello");
root.left = new Node(2, "world");
root.right = new Node(3, "!");
root.left.left = new Node(4, "2333");
}
/**
* 前序遍历
*/
public void preOrder() {
if (root == null) {
System.out.println("树为空!");
return;
}
//从根节点开始递归前序遍历
System.out.println("前序遍历为:");
preOrderRecursion(root);
}
/**
* 前序遍历 -- 递归
* @param node 节点
*/
private void preOrderRecursion(Node node) {
//打印父节点
System.out.println(node);
//左子树进行前序遍历
if (node.left != null) {
preOrderRecursion(node.left);
}
//右子树进行前序遍历
if (node.right != null) {
preOrderRecursion(node.right);
}
}
/**
* 中序遍历
*/
public void midOrder() {
if (root == null) {
System.out.println("树为空!");
return;
}
//从根节点开始递归中序遍历
System.out.println("中序遍历为:");
midOrderRecursion(root);
}
/**
* 中序遍历 -- 递归
* @param node 节点
*/
private void midOrderRecursion(Node node) {
//左子树进行中序遍历
if (node.left != null) {
midOrderRecursion(node.left);
}
//打印父节点
System.out.println(node);
//右子树进行中序遍历
if (node.right != null) {
midOrderRecursion(node.right);
}
}
/**
* 后序遍历
*/
public void postOrder() {
if (root == null) {
System.out.println("树为空!");
return;
}
//从根节点开始后序遍历
System.out.println("后序遍历为:");
postOrderRecursion(root);
}
/**
* 后序遍历 -- 递归
* @param node 节点
*/
private void postOrderRecursion(Node node) {
//左子树递归后序遍历
if (node.left != null) {
postOrderRecursion(node.left);
}
//右子树递归后续遍历
if (node.right != null) {
postOrderRecursion(node.right);
}
//打印父节点
System.out.println(node);
}
}
- (2)测试
1
2
3
4
5
6
7
8
public void binaryTreeTest() {
BinaryTree binaryTree = new BinaryTree();
binaryTree.preOrder();
binaryTree.midOrder();
binaryTree.postOrder();
}

2.3 前中后序查找
- 跟前中后序遍历思路一样,就不详细细说,只不过多了个跟数据进行对比的操作,数据一样就返回,不一样就继续遍历
- 由于前中后的基本一样,就是比较数据的位置不一样,就只写一个前序查找例子就算了
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51/**
* 通过权重前序查找数据
* @param rate 权重
*/
public void preSearch(int rate) {
if (root == null) {
System.out.println("树为空");
}
//递归前序查找数据
Node node = preSearchRecursion(rate, root);
if (node == null) {
System.out.println("查找失败!数据不存在!");
}else {
System.out.println("查找成功!数据为:" + node);
}
}
/**
* 前序查找 -- 递归
* @param rate 权重
* @param node 节点
* @return Node
*/
private Node preSearchRecursion(int rate, Node node) {
Node temp;
//比较父节点是否相等
if (node.rate == rate) {
return node;
}
//向左子树递归查找
if (node.left != null) {
temp = preSearchRecursion(rate, node.left);
if (temp != null) {
return temp;
}
}
//向右子树递归查找
if (node.right != null) {
temp = preSearchRecursion(rate, node.right);
if (temp != null) {
return temp;
}
}
//都查找不到,返回null
return null;
}
- (2)测试
1
2
3
4
5
6
public void binaryTreeTest() {
BinaryTree binaryTree = new BinaryTree();
binaryTree.preSearch(4);
}

2.4 删除
- 删除规则
- (1)删除的是叶子节点,直接删除该节点
- (2)删除的是非叶子节点,则删除该的子树(或取其中一个子节点来代替头结点)
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70/**
* 通过权重删除数据
* @param rate 权重
*/
public void delete(int rate) {
//判断根节点是否为空
if (root == null) {
System.out.println("树为空,无数据删除!");
return;
}
//判断根节点是否是删除数据
if (root.rate == rate) {
root = null;
System.out.println("删除成功!");
return;
}
//以上条件都不满足,则进行递归删除
boolean isDelete = deleteRecursion(rate, root);
if (isDelete) {
System.out.println("删除成功!");
}else {
System.out.println("删除失败!找不到数据!");
}
}
/**
* 删除节点 -- 递归
* @param rate 权重
* @param node 节点
* @return boolean
*/
private boolean deleteRecursion(int rate, Node node) {
boolean isDelete; //记录是否删除
//判断左子节点是否是删除数据
if (node.left != null && node.left.rate == rate) {
node.left = null;
return true;
}
//判断右子节点是否是删除数据
if (node.right != null && node.right.rate == rate) {
node.right = null;
return true;
}
//都不是删除数据,进行递归删除
//向左子树递归删除
if (node.left != null) {
isDelete = deleteRecursion(rate, node.left);
//已删除则退出递归
if (isDelete) {
return true;
}
}
//向右子树递归删除
if (node.right != null) {
isDelete = deleteRecursion(rate, node.right);
//已删除则退出递归
if (isDelete) {
return true;
}
}
//如果都没有退出递归,则删除失败
return false;
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
11
12
public void binaryTreeTest() {
BinaryTree binaryTree = new BinaryTree();
binaryTree.preOrder();
System.out.println();
binaryTree.delete(4);
System.out.println();
binaryTree.preOrder();
}
