树形结构之赫夫曼树的介绍和代码实现
1 赫夫曼树
1.1 介绍
- 赫夫曼树(Huffman Tree):当给树中的每个叶子节点一定的权值,来表示路径的长度。若通知这些节点的组合,形成的树的带权路径长度(wpl:weighted path length)达到最小值,此二叉树称为最优二叉树,也称为赫夫曼树(哈夫曼树,霍夫曼树)
- 特点:权值较大的节点一般离根节点比较近
- 其他概念:
- (1)路径:从一个节点到其子节点/孙子节点的道路。即经过哪些节点
- (2)路径长度:路径跨越的层数-1
- (3)节点的权:给节点赋一定值大小
- (4)带权路径长度:从根节点到该节点之间的*路径长度 * 节点的权*
- (5)树的带权路径长度:所有节点的带权路径长度之和
1.2 思路
- (1)对数组进行升序排序(从小到大)
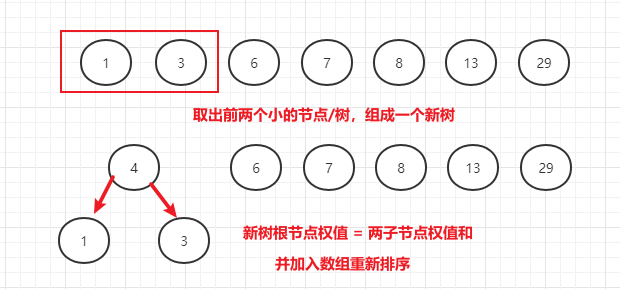
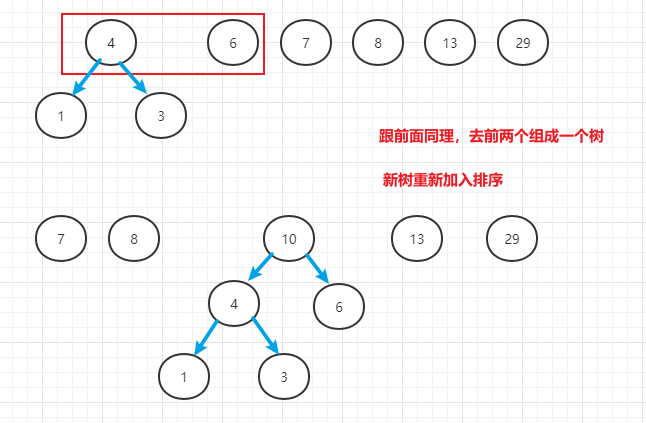
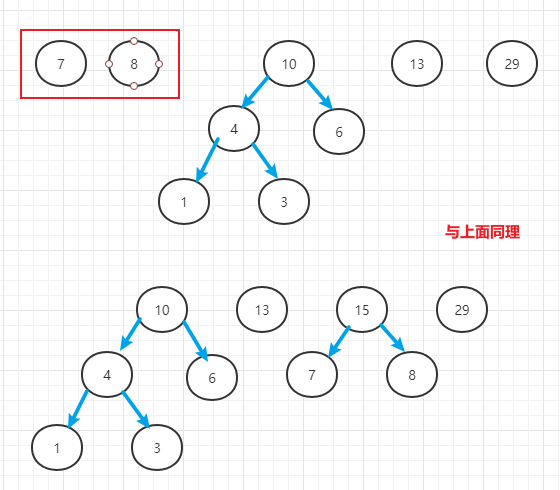
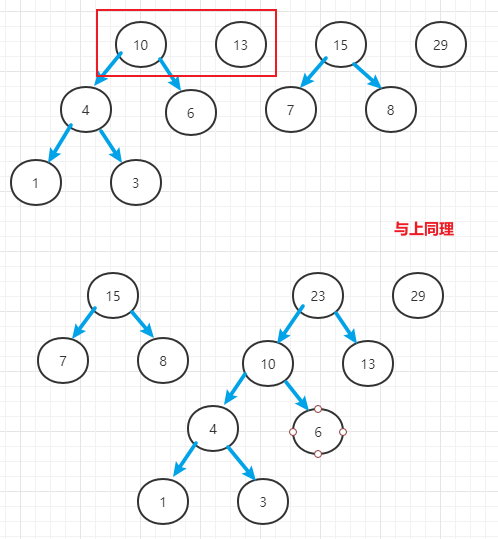
- (2)取出根节点权值前两个小的树(或节点),组成一个新二叉树
- (3)新二叉树的根节点值为其两个子节点权值之和
- (4)根节点值加入数组,重新排序,继续循环上面步骤
- 举例:将数组
[1, 3, 6, 7, 8, 13, 29]组成赫夫曼树
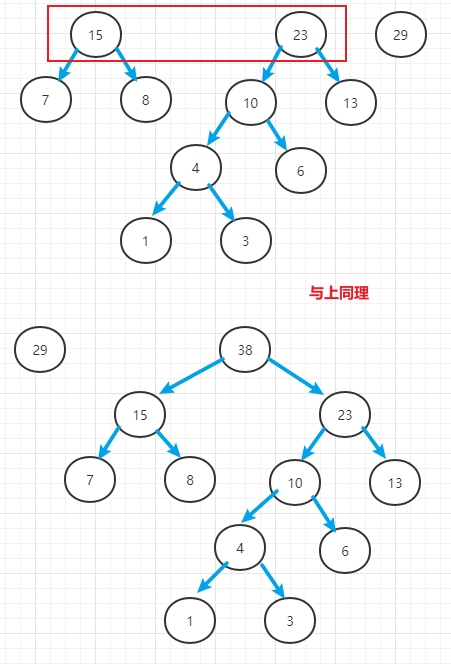
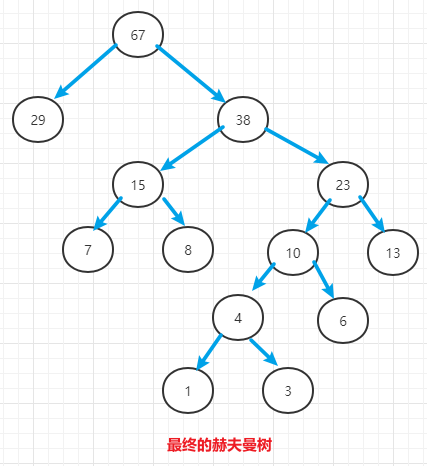
1.3 代码
- (1)代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100public class HuffmanTree {
//子类 --- 树节点
//为了让节点之间能够进行比较排序,实现Comparable接口
private class Node implements Comparable<Node> {
public int weight; //权值
public Node left; //左子节点
public Node right; //右子节点
public Node(int weight) {
this(weight, null, null);
}
public Node(int weight, Node left, Node right) {
this.weight = weight;
this.left = left;
this.right = right;
}
public String toString() {
return "Node{weight:" + weight + '}';
}
public int compareTo(Node o) {
//当前数>比较数o,返回正数
//当前数<比较数o,返回负数
//当前数=比较数o,返回0
return weight - o.weight;
}
}
//---------------------------------------------------------------------
private Node root; //根节点
//构建对象,自动调用创建赫夫曼树
public HuffmanTree(int[] arr) {
createTree(arr);
}
/**
* 创建赫夫曼树
* @param arr 数组
*/
private void createTree(int[] arr) {
//因为频繁进行插、删操作,选择链表来存储
List<Node> nodes = new LinkedList<>();
//遍历数组,创建Node并加入链表
for (int weight : arr) {
nodes.add(new Node(weight));
}
while (nodes.size() > 1) {
//node集合排序
Collections.sort(nodes);
//取出前两个节点(自动从链表中删除)
Node left = nodes.remove(0);
Node right = nodes.remove(0);
//构建新树,新树根节点权值 = 左右子节点权值之和
Node parent = new Node(left.weight + right.weight, left, right);
//将新树加入链表集合
nodes.add(parent);
}
//将创建好的赫夫曼树根节点赋值
root = nodes.get(0);
}
/**
* 前序遍历
*/
public void prePrint() {
if (root == null) {
System.out.println("树为空!");
return;
}
prePrintRecursion(root);
}
/**
* 前序遍历 --- 递归本体
* @param node 节点
*/
private void prePrintRecursion(Node node) {
System.out.println(node);
if (node.left != null) {
prePrintRecursion(node.left);
}
if (node.right != null) {
prePrintRecursion(node.right);
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
11
public void huffmanTreeTest() {
//创建数组并打乱顺序
int[] arr = new int[]{1, 6, 3, 7, 13, 8, 29};
//创建赫夫曼树
HuffmanTree huffmanTree = new HuffmanTree(arr);
//前序遍历查看
huffmanTree.prePrint();
}
