数据结构之二叉排序树的介绍和代码实现
1 二叉排序树
1.1 介绍
二叉排序树: BST(Binary Sort(Search) Tree),对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大,若拥有相同值,则随意放左子节点或右子节点
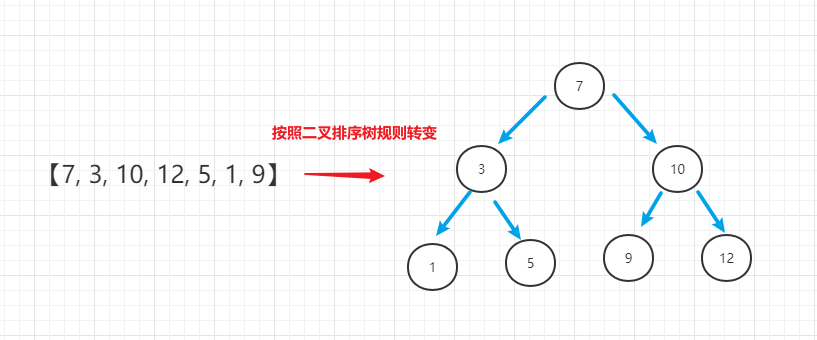
因为二叉排序树的特点,我们使用中序遍历,得出来的结果就是一个有序序列
1.2 代码
- (1)二叉排序树 - 新增与遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91public class BinarySortTree {
//子类 --- 节点
private class Node {
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
public String toString() {
return "Node{value = " + value + '}';
}
}
//----------------------------------------------------
//根节点
private Node root;
/**
* 新增数据
* @param value 值
*/
public void add(int value) {
Node node = new Node(value);
if (root == null) {
root = node;
return;
}
//递归新增数据
addRecursion(root, node);
}
/**
* 新增数据 - 递归本体
* @param node 节点
* @param newNode 新节点
*/
private void addRecursion(Node node, Node newNode) {
//当前值 < 新增值
if (node.value < newNode.value) {
//判断右子节点是否为null,null直接插入,否则向右递归找
if (node.right == null) {
node.right = newNode;
}else {
addRecursion(node.right, newNode);
}
//当前值 >= 新增值
}else {
//判断左子节点是否为null,null直接插入,否则向左递归找
if (node.left == null) {
node.left = newNode;
}else {
addRecursion(node.left, newNode);
}
}
}
/**
* 中序遍历
*/
public void infixPrint() {
if (root == null) {
System.out.println("树为空!");
return;
}
infixRecursion(root);
}
/**
* 中序遍历 - 递归本体
* @param node 节点
*/
private void infixRecursion(Node node) {
if (node.left != null) {
infixRecursion(node.left);
}
System.out.println(node);
if (node.right != null) {
infixRecursion(node.right);
}
}
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public void binarySortTreeTest() {
//创建二叉排序树
BinarySortTree binarySortTree = new BinarySortTree();
//遍历新增数据
int[] arr = new int[]{7, 3, 10, 12, 5, 1, 9};
for(int i : arr) {
binarySortTree.add(i);
}
//中序遍历
binarySortTree.infixPrint();
}
2 二叉排序树-删除
2.1 介绍
二叉排序树的删除情况要分为三种情况:
(1)删除的是叶子节点
(2)删除的是父节点,该父节点只有一个子节点
(3)删除的是父节点,该父节点有两个子节点
2.2 删除基本思路
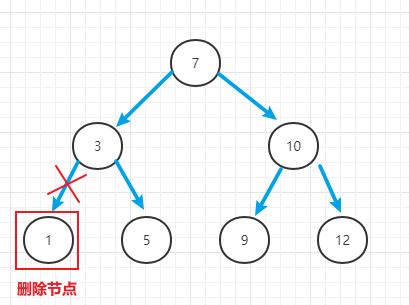
(1)删除叶子节点
找到该叶子节点的父节点,将其父节点的左/右子节点赋值为null
(2)删除只有一个子节点的节点
找到该删除节点的父节点,将其父节点的对应的删除子节点 = 该删除节点的唯一子节点
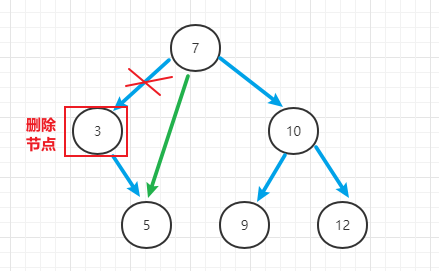
(3)删除拥有两个子节点的节点
找删除的节点的左子树中最大的值/右子树中最小的值,记录最小/最大值,再对该最小/最大值节点进行删除,将要删除的节点的值修改为记录的最小/大值
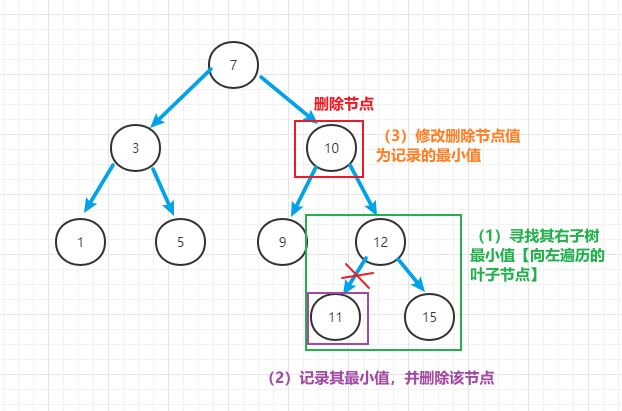
2.3 根节点特殊处理
- 上面的思路中删除叶子节点,以及删除只有一个子节点的节点都利用了目标节点的父节点,如果目标节点为根节点,那其父节点为null,会出现空指针异常,需要特殊处理
(1)删除的根节点为叶子节点
当删除的根节点为叶子节点,即整棵树只有根节点,直接将根节点设置为null即可
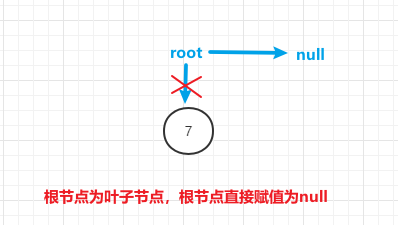
(2)删除的根节点为只有一个子节点的节点
当删除的根节点为只有一个子节点的节点,直接将根节点设置为该唯一的子节点
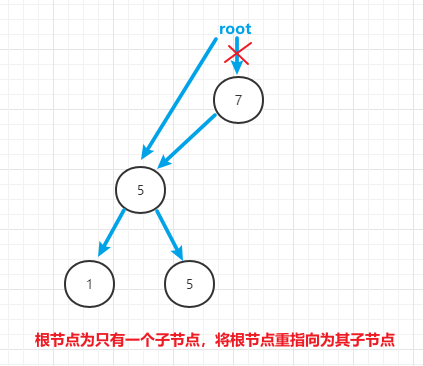
2.4 代码
- (1)代码实现【在之前写的树基础上,新增以下方法】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136/**
* 删除节点
* @param value 删除值
*/
public void delete(int value) {
//获取目标节点 和 其父节点
Map<String, Node> data = search(value);
Node parent = data.get("parent");
Node target = data.get("target");
//(1)目标节点是叶子节点
if (target.left == null && target.right == null) {
//叶子节点为根节点
if (parent == null) {
root = null;
return;
}
//通过父节点设置子节点为null
if (parent.left == target) {
parent.left = null;
}else {
parent.right = null;
}
//(2)目标节点拥有两个子节点
}else if (target.left != null && target.right != null) {
//删除右子树最小值节点,并获取返回值
int smallest = delRightSmallest(target.right);
target.value = smallest;
//(3)目标节点只有一个子节点
}else {
//获取目标节点子节点
Node temp;
if(target.left != null) {
//目标节点为根节点
if (parent == null) {
root = target.left;
return;
}
temp = target.left;
}else {
//目标节点为根节点
if (parent == null) {
root = target.right;
return;
}
temp = target.right;
}
//父节点指向目标节点的子节点
if (parent.left == target) {
parent.left = temp;
}else {
parent.right = temp;
}
}
}
/**
* 查找目标节点和其父节点
* @param value 目标节点值
* @return Node
*/
public Map<String, Node> search(int value) {
if (root == null) {
throw new RuntimeException("树为空!");
}
//目标节点为root,父节点为null
if (root.value == value) {
Map<String, Node> data = new HashMap<>();
data.put("parent", null);
data.put("target", root);
return data;
}
//递归寻找目标节点和其父节点
return searchRecursion(value, root);
}
/**
* 查找目标节点和其父节点 - 递归本体
* @param value 目标节点值
* @param node 节点
* @return Map<String, Node>
*/
private Map<String, Node> searchRecursion(int value, Node node) {
Node temp;
//目标值 > 节点值 (向右子节点找)
if (node.value < value) {
temp = node.right;
//目标值 < 节点值 (向左子节点找)
}else {
temp = node.left;
}
//左/右子节点为null,删除节点不存在,抛出异常
if (temp == null) {
throw new RuntimeException("该删除值不存在!");
}else {
//判断左/右子节点是否删除节点,是直接返回当前节点和目标节点(Map封装),否则递归寻找
if (temp.value == value) {
Map<String, Node> data = new HashMap<>();
data.put("parent", node);
data.put("target", temp);
return data;
}else {
return searchRecursion(value, temp);
}
}
}
/**
* 删除右子树最小节点,并返回最小值
* @param node 右子树根节点
* @return int
*/
private int delRightSmallest(Node node) {
Node temp = node;
//循环向左寻找最小值
while (temp.left != null) {
temp = temp.left;
}
//调用写好的删除节点方法
delete(temp.value);
return temp.value;
}
- (2)测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void binarySortTreeTest() {
//创建二叉排序树
BinarySortTree binarySortTree = new BinarySortTree();
//遍历插入数据
int[] arr = new int[]{7, 3, 10, 12, 5, 1, 9};
for(int i : arr) {
binarySortTree.add(i);
}
//随意删除节点
binarySortTree.delete(7);
binarySortTree.delete(3);
binarySortTree.delete(12);
binarySortTree.delete(9);
//中序遍历
binarySortTree.infixPrint();
}