图的遍历算法:深度优先搜索,广度优先搜索
1 深度优先遍历
1.1 介绍
深度优先搜索(Depth First Search):从初始顶点开始访问,标记为”已访问”;选择其中一个邻接顶点进行访问,设置被访问的节点为初始顶点,标记”已访问”,继续选择其中一个未访问的邻接顶点进行访问…以此类推,递归进行。直到初始节点的邻接节点没有”未访问”状态的顶点,回溯到上一个顶点,判断是否有其他未访问的顶点,进行访问。
明显深度优先算法和树的遍历,获取之前学的算法基本一致,都使用到了递归回溯方法。
1.2 图解
- (1)以此图为例,以点A为初始顶点
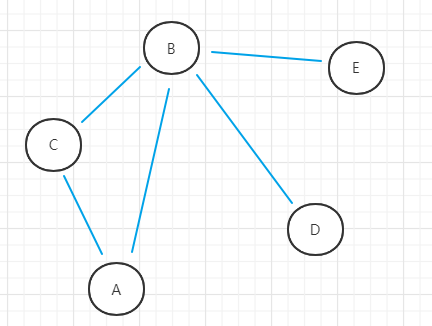
- (2)初始顶点A选择未访问顶点B,作为初始顶点
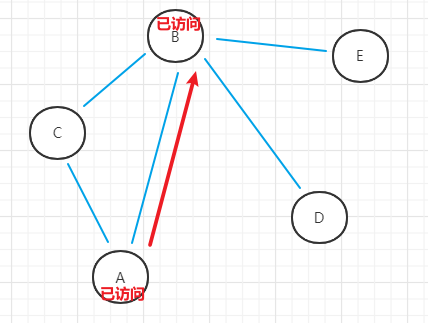
- (3)初始顶点B选择未访问顶点C,作为初始顶点
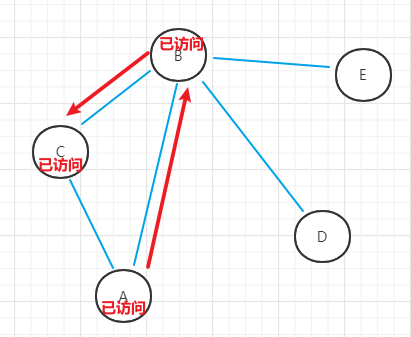
- (4)C点不存在相邻的未访问顶点,回溯到B点,选择D点作为初始顶点
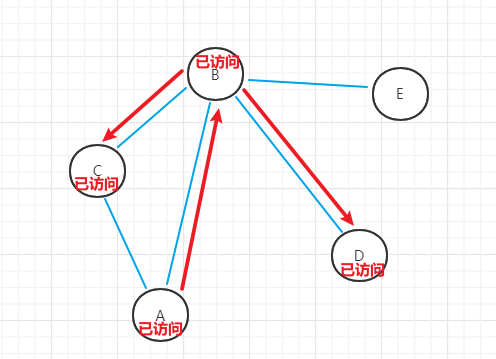
- (5)D点不存在相邻的未访问顶点,回溯到B点,选择E点作为初始顶点
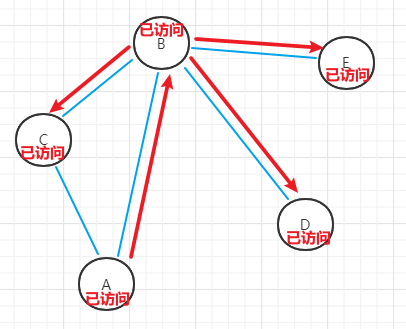
- (6)E点存在相邻未访问顶点,回溯B点;B点也不存在,回溯到A点;A点也不存在,遍历结束
1.3 代码实现
- (1)准备一个图(邻接矩阵)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60public class AdjacencyMatrix {
//顶点数组
private final Object[] vertexArr;
//邻接矩阵(二维数组)
private final int[][] matrix;
//构造器
public AdjacencyMatrix(Object[] vertexArr) {
this.vertexArr = vertexArr;
int len = vertexArr.length;
this.matrix = new int[len][len];
}
/**
* 连接两个顶点
* @param vertex1 顶点1
* @param vertex2 顶点2
*/
public void connect(Object vertex1, Object vertex2) {
int index1 = getIndex(vertex1);
int index2 = getIndex(vertex2);
//无向图(对称)
matrix[index1][index2] = 1;
matrix[index2][index1] = 1;
}
/**
* 获取顶点所在下标
* @param vertex 顶点
* @return int(下标)
*/
private int getIndex(Object vertex) {
for (int i=0; i<vertexArr.length; i++) {
if (vertexArr[i].equals(vertex)) {
return i;
}
}
throw new RuntimeException("顶点不存在,连接失败!");
}
/**
* 打印邻接矩阵
*/
public void print() {
System.out.println("邻接矩阵为:");
for(int[] row : matrix) {
for (int item : row) {
System.out.print(item + "\t");
}
System.out.println("");
}
}
}
- (2)深度优先搜索方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58/**
* 深度优先搜索
*/
public void depthFirstSearch() {
//访问标记数组(记录已访问顶点)
boolean[] visitedArr = new boolean[vertexArr.length];
//深度优先搜索 - 递归 (从0号点开始)
dfsRecursion(visitedArr, 0);
}
/**
* 深度优先搜索 - 递归本体
* @param visitedArr 访问标记数组
* @param row 初始顶点(邻接矩阵.行/列 == 顶点)
*/
private void dfsRecursion(boolean[] visitedArr, int row) {
//标记初始顶点为"已访问"
visitedArr[row] = true;
//获取下一个未访问顶点
int nextRow = getNextUnVisited(visitedArr, row);
//循环递归深度优先搜索,直至无下一个未访问顶点
while (nextRow >= 0) {
//打印初始顶点 —> 下一个未访问顶点
System.out.println(vertexArr[row] + " -> " + vertexArr[nextRow]);
//递归深度优先搜索下一个未访问顶点
dfsRecursion(visitedArr, nextRow);
//递归回溯,重新寻找下一个未访问顶点
nextRow = getNextUnVisited(visitedArr, row);
}
}
/**
* 获取下一个未访问顶点
* @param visitedArr 访问标记数组
* @param row 初始顶点(邻接矩阵.行/列 == 顶点)
* @return int
*/
private int getNextUnVisited(boolean[] visitedArr, int row) {
//遍历寻找邻接顶点(邻接矩阵为1)
for(int column=0; column<vertexArr.length; column++) {
if (matrix[row][column] > 0) {
//判断该顶点是否标记为“已访问”
if (!visitedArr[column]) {
return column;
}
}
}
//找不到,返回-1
return -1;
}
- (3)测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void dfsTest() {
//创建邻接矩阵
String[] vertexArr = new String[]{"A", "B", "C", "D", "E"};
AdjacencyMatrix adjacencyMatrix = new AdjacencyMatrix(vertexArr);
//连接顶点
adjacencyMatrix.connect("A", "B");
adjacencyMatrix.connect("A", "C");
adjacencyMatrix.connect("B", "C");
adjacencyMatrix.connect("B", "D");
adjacencyMatrix.connect("B", "E");
//深度优先搜索
adjacencyMatrix.depthFirstSearch();
}
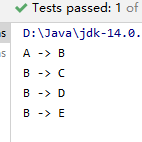
2 广度优先遍历
2.1 介绍
广度优先搜索(Broad First Search):将一个初始顶点加入到队列中,然后将该初始顶点的所有邻接顶点都加入到队列中,直到无邻接顶点,此时初始顶点出列。新的初始顶点变为队列的队首,重复上面的操作,以此类推,直到队列为空,搜索结束。
若按邻接矩阵来理解,就相当于一行一行的寻找全部未访问的邻接顶点
2.2 图解
- (1)以此图为例,A作为初始顶点

- (2)将A点所有邻接顶点加入队列,标记为已访问,并A点出队列
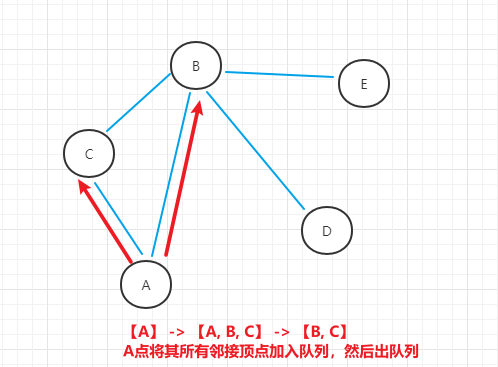
- (3)将B点所有邻接顶点接入队列,标记为已访问,并B点出队列
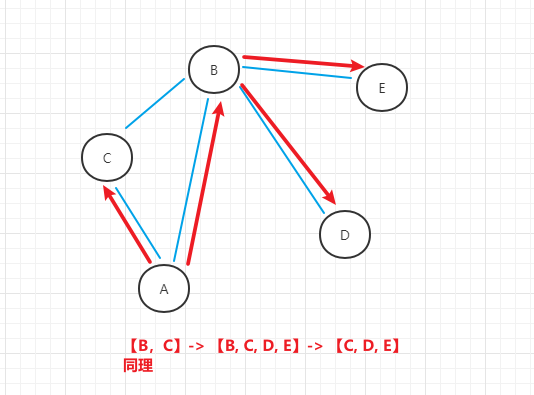
- (4)C,D,E点都没有邻接顶点,依次出队列,队列为空,搜索结束
2.3 代码实现
- (1)准备图(邻接矩阵),可看上面的深度优先遍历
- (2)广度优先搜索方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72/**
* 广度优先搜索
*/
public void BoardFirstSearch() {
//标记已访问数组
boolean[] visitedArr = new boolean[vertexArr.length];
//用linkedList来代替队列,并添加初始顶点0,标记为已访问
List<Integer> queue = new LinkedList<>();
queue.add(0);
visitedArr[0] = true;
//广度优先搜索 - 循环
bfsCirculation(queue, visitedArr);
}
/**
* 广度优先搜索 - 循环本体
* @param queue 队列
* @param visitedArr 标记已访问数据
*/
private void bfsCirculation(List<Integer> queue, boolean[] visitedArr) {
//队首
Integer head;
//下一个未访问邻接顶点
int nextRow;
//队列为空,结束循环
while (queue.size() > 0) {
head = queue.get(0);
nextRow = getNextUnVisited(visitedArr, head);
//队首没有未访问顶点时,结束循环
while (nextRow > 0) {
System.out.println(vertexArr[head] + " -> " + vertexArr[nextRow]);
//标记为已访问
visitedArr[nextRow] = true;
//入列
queue.add(nextRow);
//继续通过队首寻找下一个未访问顶点
nextRow = getNextUnVisited(visitedArr, head);
}
//出列
queue.remove(0);
}
}
/**
* 获取下一个未访问顶点
* @param visitedArr 访问标记数组
* @param row 初始顶点(邻接矩阵.行/列 == 顶点)
* @return int
*/
private int getNextUnVisited(boolean[] visitedArr, int row) {
//遍历寻找邻接顶点(邻接矩阵为1)
for(int column=0; column<vertexArr.length; column++) {
if (matrix[row][column] > 0) {
//判断该顶点是否标记为“已访问”
if (!visitedArr[column]) {
return column;
}
}
}
//找不到,返回-1
return -1;
}
- (3)测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public void bfsTest() {
//创建邻接矩阵
String[] vertexArr = new String[]{"A", "B", "C", "D", "E"};
AdjacencyMatrix adjacencyMatrix = new AdjacencyMatrix(vertexArr);
//连接顶点
adjacencyMatrix.connect("A", "B");
adjacencyMatrix.connect("A", "C");
adjacencyMatrix.connect("B", "C");
adjacencyMatrix.connect("B", "D");
adjacencyMatrix.connect("B", "E");
//广度优先搜索
adjacencyMatrix.BoardFirstSearch();
}