【数据结构和算法】分治算法

算法之分治算法的介绍，以及简单应用实现

---

1 分治算法

1.1 介绍

分治算法（Divide and conquer algorithm）：顾明思义，“分而治之”，即将一个问题，分为很多个小问题，逐个解决，从而使得问题的解决变得简单。

基本步骤：
分解：将原问题分解为若干和规模较小，相互独立，与原问题形式相同的子问题
解决：若子问题规模较小而容易被解决，则直接解决，否则递归地解决各个子问题
合并：将各个子问题的解合并为原问题的解

应用场景：
二分搜索
大整数乘法
棋盘覆盖
归并排序
快速排序
线性时间选择
最接近点对问题
循环赛日程表
汉诺塔

---

2 汉诺塔问题

2.1 思路：

• （1）盘子只有一个，直接将盘子从开始柱子，移动到目标柱子
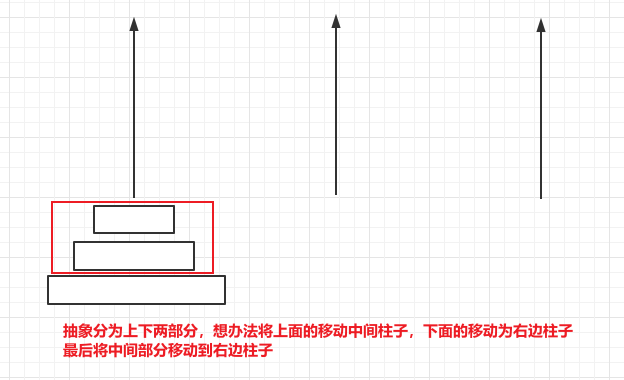
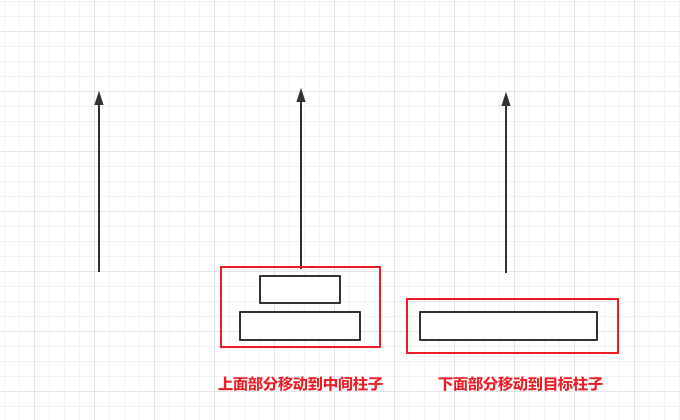
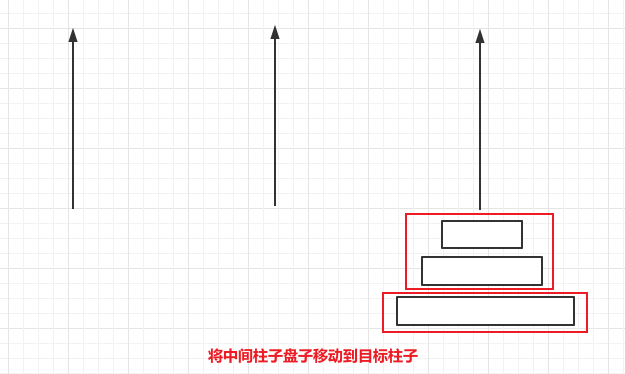
• （2）盘子大于一个，将盘子分为上下两部分。将上面的部分移动到中间柱子 （移动目的地变成中间柱子），下面部分移动到目标柱子，最后将中间柱子的盘子移动到目标柱子

2.2 图解

2.3 代码实现

• （1）代码

  /**
   * 汉诺塔问题
   * @author letere
   * @create 2021-06-05 16:33
   */
  public class HanoiTower {
      /**
       * 移动盘子（递归）
       * @param num 盘子个数
       * @param start 盘子开始柱子
       * @param target 盘子移动的目的地柱子
       * @param temp 中间柱子
       */
      public static void move(int num, char start, char target, char temp) {
          //盘子只有一个，直接从开始位置，移动到目的地
          if (num == 1) {
              System.out.println(start + " -> " + target);
              return;
          }
  
          //盘子 > 1，分为上下两部分，递归处理
          //上面部分从start柱子移动到temp柱子
          move(num-1, start, temp, target);
  		
          //下面部分从start柱子移动到target柱子
          move(1, start, target, temp);
  		
          //最后把上面部分从temp柱子移动到target柱子
          move(num-1, temp, target, start);
      }
  }

• （2）测试

  @Test
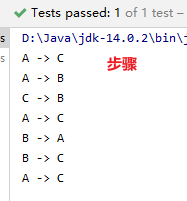
  public void hanoiTowerTest() {
  	//三个盘子，从A柱移动到C柱，中间柱子为B
  	HanoiTower.move(3, 'A', 'C', 'B');
  }