算法之KMP算法的介绍与实现
1 暴力匹配算法
1.1 介绍
暴力匹配:遍历字符串,一旦发现相似的字符,就进行匹配,匹配失败则回到发现的位置,继续往后匹配,直到匹配成功或字符串遍历完毕,匹配失败
1.2 思路
整体思路比较简单,需要注意的点是,如果匹配失败,如何返回一开始匹配的位置。因为匹配字符串都是默认保持在0号位,直到匹配成功后才往后移动。所以匹配字符串的下标就是匹配移动的长度,只要将这长度减回去,就恢复到原来的长度匹配的位置。
1.3 代码
- (1)暴力匹配方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36/**
* 暴力匹配
* @param s1 字符串1(被匹配字符串)
* @param s2 字符串2(目标字符串)
* @return int
*/
public static int violentMatch(String s1, String s2) {
//转成字符数组(方便遍历)
char[] s1Arr = s1.toCharArray();
char[] s2Arr = s2.toCharArray();
//index1记录字符串1的索引下标
int index1 = 0;
//index2记录字符串2的索引下标
int index2 = 0;
while (index1 < s1Arr.length && index2 < s2Arr.length) {
//字符串匹配
if (s1Arr[index1] == s2Arr[index2]) {
index1++;
index2++;
//匹配失败,恢复原来长度,并向后移一位
}else {
index1 = index1 - index2 + 1;
index2 = 0;
}
}
//匹配字符到达数组长度,匹配成功,返回开始匹配位置
if (index2 == s2Arr.length) {
return index1 - index2;
}
//匹配失败,返回-1
return -1;
}
- (2)测试
1
2
3
4
5
6
7
public void KMPTest() {
String s1 = "你不不不你好啊你秀秀秀";
String s2 = "你好";
int i = KMP.violentMatch(s1, s2);
System.out.println(i); //答案为4
}
2 KMP算法
2.1 介绍
KMP算法:是一个解决字符串是否在文本中出现过,若出现过,则返回最早出现的位置。因为此算法由三个人联合发表,KMP这是这三人的首字母组合。与暴力匹配不同在于,匹配不同时,会考虑匹配是否出现前后缀对称的字符,来决定匹配失败后重新匹配的位置。
2.2 思路
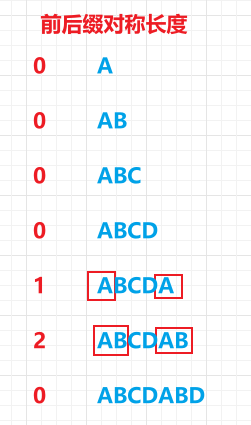
1、KMP算法核心,就是前后缀对称数组,如下图
- 求出前后缀对称数组思路
- (1)准备两个变量,一个为 len ,用来记录前后缀对称字符的长度以及对称比较指针;另一个变量 i 用于指向字符数组,来遍历比较。下面假设 字符数组为strArr[] , 前后缀对称数组为next[]
- (2)前后对称数组的0号位,一定为0,因为一个字符不存在前后缀的情况,所以字符数组遍历从1号位开始
- (3)字符比较通过 strArr[i] == str[len] 来决定
- (4)匹配成功,则 len+1 ,即表示前后缀字符长度+1,也表示下一次对称比较从下一个字符进行对比,然后记录前后缀对称数组 next[i] = len
- (5)匹配失败,则 len = next[len-1] ,意思为当前字符不存在对称情况,如果还可能出现对称情况,只能从 当前对称字符串的子对称字符串去匹配 ,一直递归往子对称字符找,要么找到成功匹配的。要么len=0,已经没有子对称的可以寻找
- (6)上面的 len = next[len-1] 是kmp算法的核心,比较难理解,推荐和此博客文章进行理解:https://blog.csdn.net/yearn520/article/details/6729426
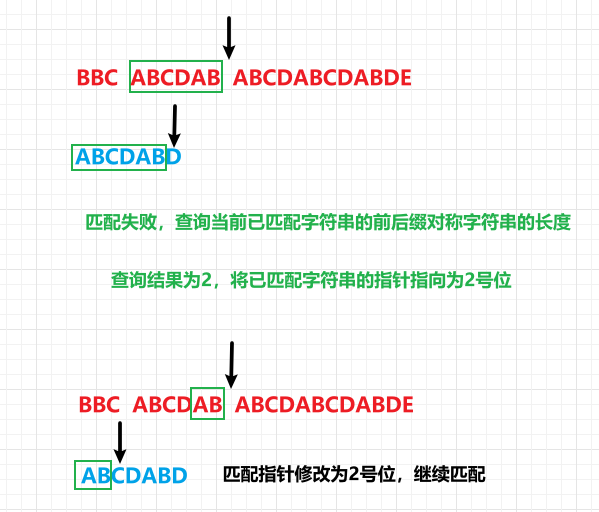
2、利用前后缀对称数组,在遍历的匹配失败的时候合理复原遍历的位置,如下图
2.3 代码
- (1)KMP匹配方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78/**
* KMP匹配
* @param str1 字符串1(被匹配字符串)
* @param str2 字符串2(模式串)
* @return int
*/
public static int kmpMatch(String str1, String str2) {
//获取前后缀对称长度数组
int[] next = getNextArr(str2);
//字符数组(方便遍历)
char[] s1Arr = str1.toCharArray();
char[] s2Arr = str2.toCharArray();
//遍历字符数组下标
int index1 = 0;
int index2 = 0;
//遍历字符数组
while(index1 < s1Arr.length && index2 < s2Arr.length) {
//匹配成功
if (s1Arr[index1] == s2Arr[index2]) {
index1++;
index2++;
}else {
//匹配失败
if (index2 > 0) {
index2 = next[index2-1];
}else {
index1++;
}
}
}
//全部匹配成功,返回开始匹配下标
if (index2 == s2Arr.length) {
return index1 - index2;
}
//失败返回-1
return -1;
}
/**
* 获取前后缀对称数组
* @param str 字符串
*/
private static int[] getNextArr(String str) {
//字符数组
char[] strArr = str.toCharArray();
//前后缀对称长度数组
int[] next = new int[str.length()];
//0号位一定为0
next[0] = 0;
//前后缀对称字符串长度
int len = 0;
//遍历字符串,从1号位开始
for(int i=1; i<str.length(); i++) {
//匹配成功,前后缀对称长度+1
if (strArr[i] == strArr[len]) {
len++;
}else {
//匹配失败,递归寻找子对称是否匹配成功
while (len > 0 && strArr[i] != strArr[len]) {
len = next[len-1];
}
}
//记录长度
next[i] = len;
}
return next;
}
- (2)测试
1
2
3
4
5
6
7
8
public void KMPTest2() {
String s1 = "BBC ABCDAB ABCDABCDABDE";
String s2 = "ABCDABD";
int i = KMP.kmpMatch(s1, s2);
System.out.println(i); //答案为15
}