【数据结构和算法】最小生成树算法

算法之最小生成树算法，最小生成树算法分为普里姆算法以及克鲁斯卡尔算法

1 最小生成树算法

1.1 介绍

最小生成树MST（Minimun Cost Spanning Tree）：给定一个带权的无向连通图，如何选取一棵生成树，使树上所有边上权的总和为最小，称为最小生成树。

特点：
- （1）N个顶点，一定有N-1条边
- （2）含有全部顶点
- （3）N-1条边都在图中【每个顶点之间可以相互到达】

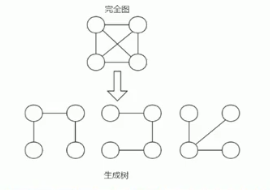
最小生成树算法：主要为普里姆算法和克鲁斯卡尔算法

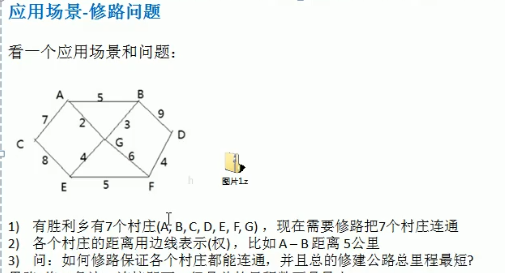
1.2 最小生成树问题

2 普里姆算法

2.1 介绍

普里姆算法（Prim）：选择一个点作为初始起点，将此点加入为已访问数组中，找出已访问数组中所有相邻的顶点，选择其中权重最小的顶点，并加入到已访问数组中。重复上面操作，直到已访问数组的长度等于顶点的个数停止。

2.2 图解

（1）以上面修路问题的图作为例子

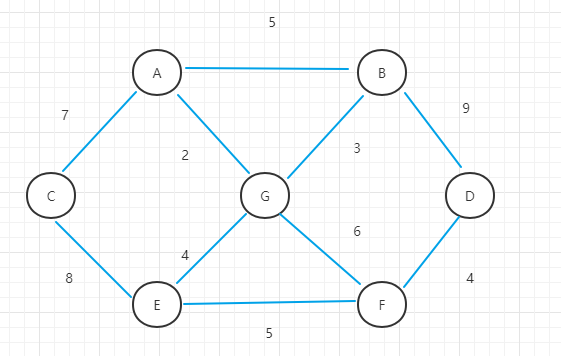
（2）选择A点作为初始顶点，加入到已访问顶点中，并寻找出A点最短权重的边

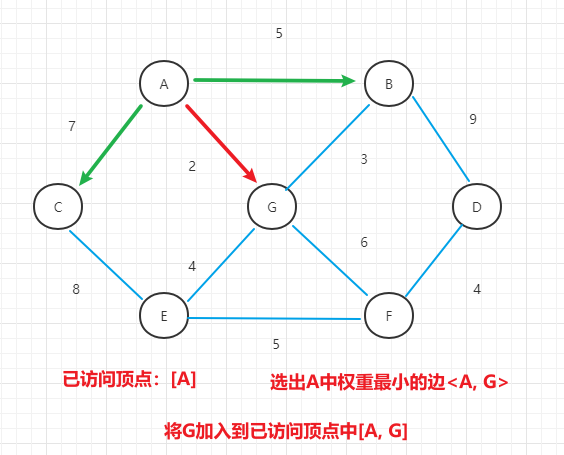
（3）按照上面的思路，选中A, G点中最短权重的边

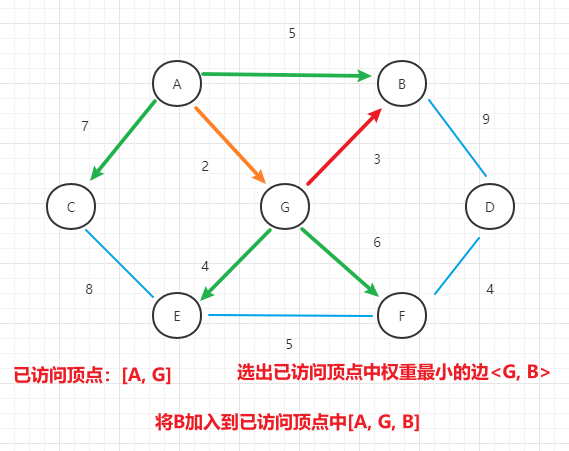
（4）按照上面的思路一路下来，最终结果为：

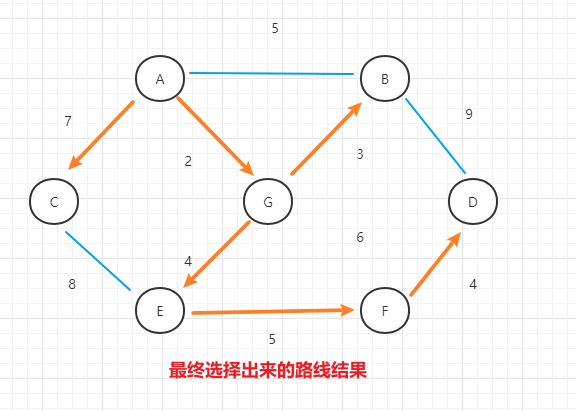
2.3 代码

（1）图类（邻接矩阵）

/**
 * 图（邻接矩阵）
 * @author letere
 * @create 2021-06-09 16:54
 */
public class Graph {
    //顶点集合
    private String[] vertexes;
    //邻接矩阵
    private int[][] matrix;
    //边个数
    private int edgeCount;

    //构造器
    public Graph(String[] vertexes) {
        this.vertexes = vertexes;

        int temp = vertexes.length;
        this.matrix = new int[temp][temp];
    }


    /**
     * 连接顶点
     * @param vertex1 顶点1
     * @param vertex2 顶点2
     * @param weight 边权重
     */
    public void connect(String vertex1, String vertex2, int weight) {
        int index1 = getVertexIndex(vertex1);
        int index2 = getVertexIndex(vertex2);

        matrix[index1][index2] = weight;
        matrix[index2][index1] = weight;

        //边个数+1
        edgeCount++;
    }


    /**
     * 获取顶点下标
     * @param vertex 顶点
     */
    private int getVertexIndex(String vertex) {
        for (int i=0; i<vertexes.length; i++) {
            if (vertex.equals(vertexes[i])) {
                return i;
            }
        }
        return -1;
    }


    /**
     * 获取顶点集合
     * @return String[]
     */
    public String[] getVertexes() {
        return vertexes;
    }


    /**
     * 获取邻接矩阵
     * @return int[][]
     */
    public int[][] getMatrix() {
        return matrix;
    }


    /**
     * 获取边个数
     * @return int
     */
    public int getEdgeCount() {
        return edgeCount;
    }
}

（2）修路问题，普里姆算法

/**
 * @author letere
 * @create 2021-06-09 16:30
 */
public class BuildRoad {
    //顶点集合
    String[] vertexes;
    //邻接矩阵
    int[][] matrix;


    //构造器
    public BuildRoad(Graph graph) {
        this.vertexes = graph.getVertexes();
        this.matrix = graph.getMatrix();
    }


    /**
     * 普里姆算法
     */
    public void primAlgorithm() {
        //已访问顶点
        List<Integer> visitedVertexes = new ArrayList<>();
        visitedVertexes.add(0);
        //连接策略（边）
        List<String> strategy = new ArrayList<>();
        //总权重
        int total = 0;

        //图已全部连通：边 = 顶点数-1
        while (strategy.size() < vertexes.length-1) {
            int index1 = -1;
            int index2 = -1;
            int min = 100000; //初始化一个巨大值，方便寻找最小值

            for (Integer row : visitedVertexes) {
                int column = 0;
                for (int weight : matrix[row]) {
                    //是邻接顶点 && 权重<最小权重 && 是未访问顶点
                    if (weight > 0 && weight < min && !visitedVertexes.contains(column)) {
                        //记录下标和最小值
                        index1 = row;
                        index2 = column;
                        min = weight;
                    }
                    column ++;
                }
            }

            //记录总权重，选择策略，已访问顶点
            total += min;
            strategy.add("<" + vertexes[index1] + ", " + vertexes[index2] + ">  权重：" + min);
            visitedVertexes.add(index2);
        }

        //打印数据
        for (String item : strategy) {
            System.out.println(item);
        }
        System.out.println("总权重为：" + total);
    }
}

（3）测试

@Test
public void primTest() {
	Graph graph = getData();

	BuildRoad buildRoad = new BuildRoad(graph);

	buildRoad.primAlgorithm();
}

/**
 * 获取数据（邻接矩阵）
 * @return buildRoad
 */
public Graph getData() {
	String[] vertexes = new String[]{"A", "B", "C", "D", "E", "F", "G"};

	Graph graph = new Graph(vertexes);
	graph.connect("A", "B", 5);
	graph.connect("A", "C", 7);
	graph.connect("A", "G", 2);
	graph.connect("B", "D", 9);
	graph.connect("B", "G", 3);
	graph.connect("C", "E", 8);
	graph.connect("D", "F", 4);
	graph.connect("E", "F", 5);
	graph.connect("E", "G", 4);
	graph.connect("F", "G", 6);

	return graph;
}

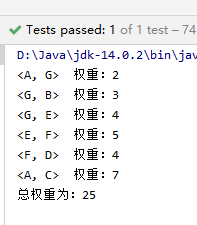
3 克鲁斯卡尔算法

3.1 介绍

克鲁斯卡尔（Krukal）算法：记录该图中所有边的权重，对边进行排序，然后从小到大选择边，加入到选择策略。选择边的时候，要注意不要形成回路。形成回路，意味着节点重复访问了。

形成回路判断：弄一个终点数组，记录每一个顶点指向下一个顶点的下标，-1表示没有下一个顶点，即为终点。当尝试加入一条边时，比较边的两个顶点的终点是否一样，一样则表示路线已连通，再进行连接会形成回路

3.2 图解

（1）还是上面修路问题的图作为例子：

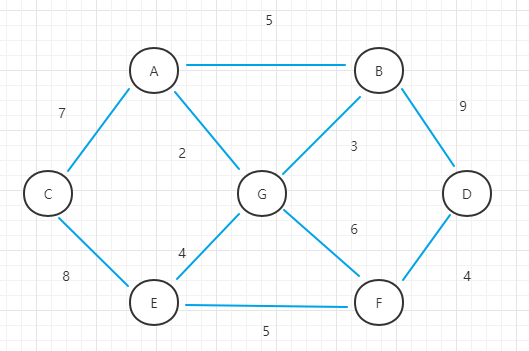
（2）选择不形成回路的最短边<A, G>，终点数组修改A指向G

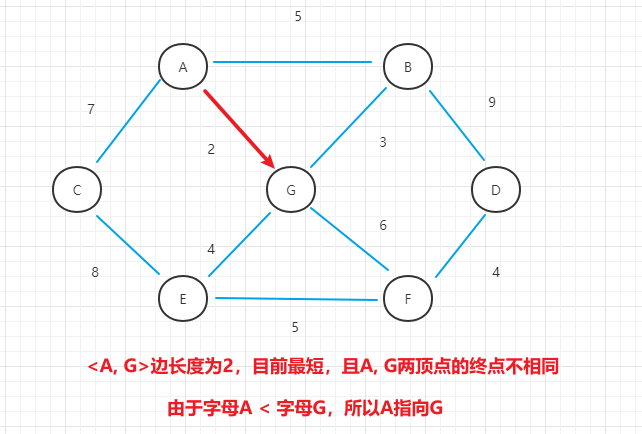
（3）继续按照上面思路，选择<B, G>，终点数组修改为B指向G

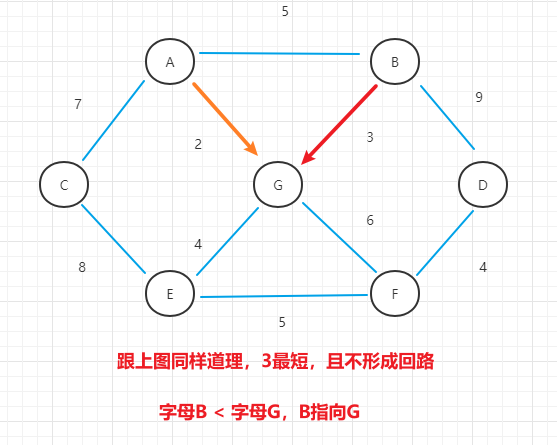
（4）最终的结果图为：

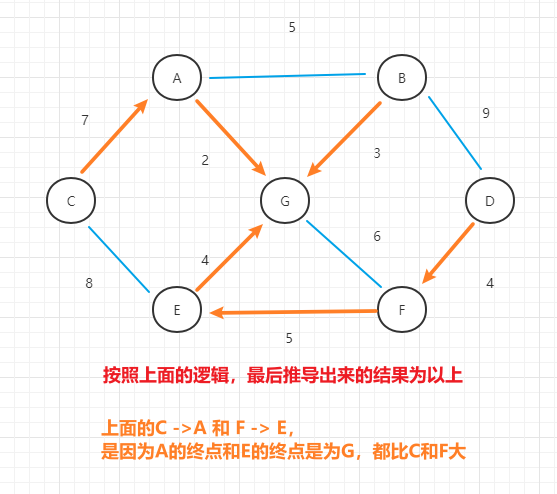
3.3 代码

（1）准备一个图类，在上面的prim算法有，不再重复写

（2）修路问题-克鲁斯卡尔算法类

/**
 * 克鲁斯卡尔算法
 * @author letere
 * @create 2021-06-11 17:11
 */
public class BuildRoad2 {
    
    /**
     * 私有子类：边
     * 实现比较接口，方便排序
     */
    private class Edge implements Comparable<Edge>{
        int start; //边顶点1
        int end; //边顶点2
        int weight; //权重

        public Edge(int start, int end, int weight) {
            this.start = start;
            this.end = end;
            this.weight = weight;
        }

        @Override
        public int compareTo(Edge o) {
            return weight - o.weight;
        }
    }

//--------------------------------------------------------------------------

    //顶点数组
    private final String[] vertexes;
    //邻接矩阵
    private final int[][] matrix;
    //边数组
    private final Edge[] edges;


    //构造器
    public BuildRoad2(Graph graph) {
        this.vertexes = graph.getVertexes();
        this.matrix = graph.getMatrix();
        edges = new Edge[graph.getEdgeCount()];

        int len = vertexes.length;
        int temp = 0;
        //初始化边数组
        //上倒三角遍历，可以过滤重复的边，并且边的顶点按顶点数组的大小
        for (int i=0; i<len; i++) {
            for (int j=i; j<len; j++) {
                if (matrix[i][j] > 0) {
                    edges[temp] = new Edge(i, j, matrix[i][j]);
                    temp ++;
                }
            }
        }
    }


    /**
     * 克鲁斯卡尔算法
     */
    public void kruskal() {
        //终点数组：记录每个顶点的下一个顶点的下标，数值为-1则表示终点（没有下一个顶点）
        int[] ends = new int[vertexes.length];
        for (int i=0; i<vertexes.length; i++) {
            ends[i] = -1;
        }

        //选择策略（边集合）
        List<String> strategy = new ArrayList<>();
        //总权重
        int total = 0;

        //对边按权重大小进行排序
        Arrays.sort(edges);

        //循环寻找选择策略
        while (strategy.size() < vertexes.length-1) {

            for (Edge edge : edges) {
                //求出边的两个顶点对应的终点
                int endIndex1 = getEnd(ends, edge.start);
                int endIndex2 = getEnd(ends, edge.end);

                //对比两顶点的终点是否一致（一致则形成回路）
                if (endIndex1 != endIndex2) {
                    //判断哪个终点大，来修改终点数组（选择谁指向谁）
                    if (endIndex1 <= endIndex2) {
                        ends[edge.start] = edge.end;
                        strategy.add("<" + vertexes[edge.start] + ", " + vertexes[edge.end] + ">：" + edge.weight);
                    }else {
                        ends[edge.end] = edge.start;
                        strategy.add("<" + vertexes[edge.end] + ", " + vertexes[edge.start] + ">：" + edge.weight);
                    }

                    total += edge.weight;
                    break;
                }
            }
        }

        //打印结果
        for (String edge : strategy) {
            System.out.println(edge);
        }
        System.out.println("总权重：" + total);
    }


    /**
     * 获取当前顶点的终点下标
     * @param ends 终点数组
     * @param index 顶点下标
     * @return int
     */
    private int getEnd(int[] ends, int index) {
        //值 != -1，不是终点，对指向的下一个顶点进行判断，直到找出终点
        while (ends[index] != -1) {
            index = ends[index];
        }

        return index;
    }
}

（3）测试

@Test
public void kruskalTest() {
	Graph graph = getData();

	BuildRoad2 buildRoad = new BuildRoad2(graph);

	buildRoad.kruskal();
}

/**
 * 获取数据（邻接矩阵）
 * @return buildRoad
 */
public Graph getData() {
	String[] vertexes = new String[]{"A", "B", "C", "D", "E", "F", "G"};

	Graph graph = new Graph(vertexes);
	graph.connect("A", "B", 5);
	graph.connect("A", "C", 7);
	graph.connect("A", "G", 2);
	graph.connect("B", "D", 9);
	graph.connect("B", "G", 3);
	graph.connect("C", "E", 8);
	graph.connect("D", "F", 4);
	graph.connect("E", "F", 5);
	graph.connect("E", "G", 4);
	graph.connect("F", "G", 6);

	return graph;
}