【数据结构和算法】最短路径算法

最短路径算法的介绍和代码实现

---

1 最短路径算法

1.1 问题

---

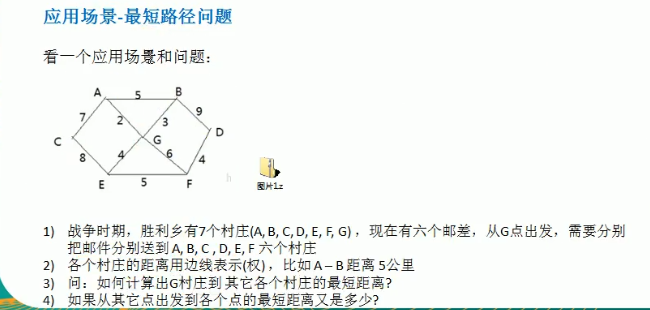
2 迪杰斯特拉算法

2.1 介绍

迪杰斯特拉（Dijkstra）算法：是典型的最短路径算法，用于计算一个顶点到其他顶点的最短路径。它主要特点为一起始点为中心向外层次扩展（广度优先遍历思想），直到全部顶点都被遍历过

2.2 思路

• （1） 创建两个数组，一个已访问顶点数组（visitedArr），用来记录哪些顶点已被访问；另一个是最短路径数组（distanceArr），记录选定顶点到各个顶点之间的最短路径，数组初始化为-1，表示顶点之间不连通，没有最短路径。

• （2） 选定一个顶点作为初始顶点（第一次的初始顶点也是选定顶点），记录该顶点为已访问，若该顶点的距离数组为-1，则此顶点是选定顶线，修改为0，表示顶点到自身的距离设置为0

• （3） 将初始顶点的相邻的未访问顶点记录，先计算路径：（选定节点到初始顶点距离 + 初始顶点到相邻未访问顶点距离），比较距离数组中未访问顶点的最短路径。若为-1，则是第一连通，直接距离数据赋值。不为-1，则此顶点之前已被连通，现在的是另一种连通路线，比较路径大小。比已记录的最短路径要小，则修改距离数组。

• （4） 从距离数组选取路径最短，并且是未访问的顶点，作为新的初始顶点。重复（2）（3）（4）的步骤

• （5） 直到所有顶点表示为已访问时，结束算法

2.3 图解

• （1）以此图为例

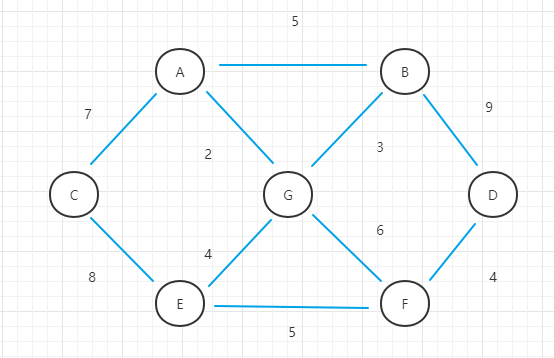
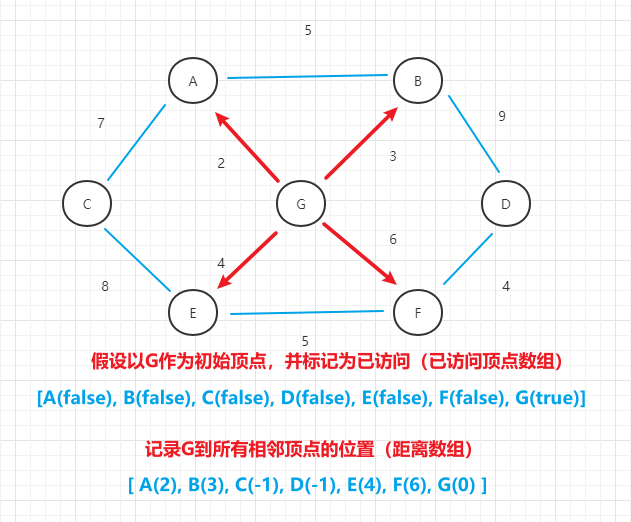
• （2）以G点作为初始顶点，开始算法

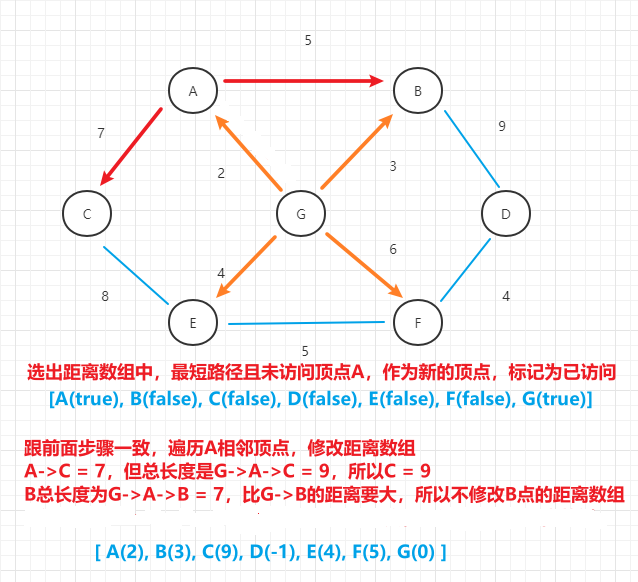
• （3）以A点继续作为初始顶点，对比相邻未访问顶点的距离

• （4）以上面的情况推出得到的结果为：

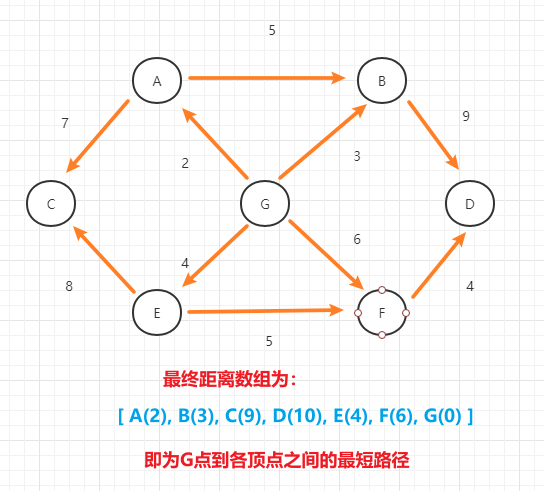
2.4 代码

• （1）图类

  /**
   * 图（邻接矩阵）
   * @author letere
   * @create 2021-06-09 16:54
   */
  public class Graph {
      //顶点集合
      private String[] vertexes;
      //邻接矩阵
      private int[][] matrix;
      //边个数
      private int edgeCount;
  
      //构造器
      public Graph(String[] vertexes) {
          this.vertexes = vertexes;
  
          int temp = vertexes.length;
          this.matrix = new int[temp][temp];
      }
  
  
      /**
       * 连接顶点
       * @param vertex1 顶点1
       * @param vertex2 顶点2
       * @param weight 边权重
       */
      public void connect(String vertex1, String vertex2, int weight) {
          int index1 = getVertexIndex(vertex1);
          int index2 = getVertexIndex(vertex2);
  
          matrix[index1][index2] = weight;
          matrix[index2][index1] = weight;
  
          //边个数+1
          edgeCount++;
      }
  
  
      /**
       * 获取顶点下标
       * @param vertex 顶点
       */
      private int getVertexIndex(String vertex) {
          for (int i=0; i<vertexes.length; i++) {
              if (vertex.equals(vertexes[i])) {
                  return i;
              }
          }
          return -1;
      }
  
  
      /**
       * 获取顶点集合
       * @return String[]
       */
      public String[] getVertexes() {
          return vertexes;
      }
  
  
      /**
       * 获取邻接矩阵
       * @return int[][]
       */
      public int[][] getMatrix() {
          return matrix;
      }
  
  
      /**
       * 获取边个数
       * @return int
       */
      public int getEdgeCount() {
          return edgeCount;
      }
  }

• （2）最短路径问题类

  /**
   * 最短路径问题 - 迪杰斯特拉算法
   * @author letere
   * @create 2021-06-15 21:31
   */
  public class ShortestPath {
      //顶点数组
      private final String[] vertexArr;
      //邻接矩阵
      private final int[][] matrix;
  
      //构造器
      public ShortestPath(Graph graph) {
          this.vertexArr = graph.getVertexes();
          this.matrix = graph.getMatrix();
      }
  
  
      /**
       * 迪杰斯特拉算法
       * @param vertex 初始顶点
       */
      public void dijkstra(String vertex) {
          //已访问顶点数组
          boolean[] visitedArr = new boolean[vertexArr.length];
  
          //距离数组（记录初始顶点到每个顶点最短距离）
          int[] distanceArr = new int[vertexArr.length];
          Arrays.fill(distanceArr, -1);
  
          //前驱顶点数组（记录路线）
          int[] preVertexArr = new int[vertexArr.length];
          Arrays.fill(preVertexArr, -1);
  
          //初始顶点下标并修改距离数组
          int startIndex = getVertexIndex(vertex);
          distanceArr[startIndex] = 0;
  
          //最短路径长度
          int len;
          int row = startIndex;
  
          //当下一未访问最短路径顶点存在，继续循环（-1表示不存在）
          while (row != -1) {
              visitedArr[row] = true;
  
              //遍历行中元素（列）
              for (int column=0; column<matrix[row].length; column++) {
                  //是相邻顶点
                  if (matrix[row][column] > 0) {
                      //计算叠加后的路径（选定顶点到初始顶点距离 + 初始顶点到相邻顶点的距离）
                      len = distanceArr[row] + matrix[row][column];
  
                      //记录初始顶点到当前相邻顶点的路径
                      //（-1为未访问过，直接赋值，反之跟之前的路径比较是否更短，更短才重新赋值）
                      if (distanceArr[column] == -1) {
                          distanceArr[column] = len;
                          preVertexArr[column] = row;
                      }else if (len < distanceArr[column]) {
                          distanceArr[column] = len;
                          preVertexArr[column] = row;
                      }
                  }
              }
  
              //获取下一个未访问最短路径的顶点
              row = getNextVertex(visitedArr, distanceArr);
          }
  
          //打印结果
          print(distanceArr, preVertexArr);
      }
  
  
      /**
       * 获取顶点下标
       * @param vertex 顶点
       * @return int
       */
      private int getVertexIndex(String vertex) {
          for (int i=0; i<vertexArr.length; i++) {
              if (vertexArr[i].equals(vertex)) {
                  return i;
              }
          }
          return -1;
      }
  
  
      /**
       * 获取下一个路径最短的新访问顶点
       * @param visitedArr 已访问顶点数组
       * @param distanceArr 距离数组
       * @return int
       */
      private int getNextVertex(boolean[] visitedArr, int[] distanceArr) {
          int min = 0;
          int index = -1;
          //遍历寻找，最短路径的顶点，作为下一个访问顶点
          for (int i=0; i<visitedArr.length; i++) {
              if (distanceArr[i] > 0) {
                  //属于未访问顶点
                  if (!visitedArr[i]) {
                      //赋初值
                      if (min == 0) {
                          min = distanceArr[i];
                          index = i;
                      }
  
                      //当前路径 < 暂时最短路径，覆盖暂时最短路径，并记录下标
                      if (distanceArr[i] < min) {
                         min = distanceArr[i];
                         index = i;
                      }
                  }
              }
          }
  
          return index;
      }
  
  
      /**
       * 打印最短路径信息
       * @param distanceArr 路径数组
       * @param preVertexArr 前驱顶点数组
       */
      private void print(int[] distanceArr, int[] preVertexArr) {
          //选择策略
          String[] strategies = new String[distanceArr.length];
          String strategy;
  
          //利用前驱顶点数组寻找最短路径路线
          int index;
          for (int i=0; i<preVertexArr.length; i++) {
              strategy = vertexArr[i];
              index = i;
              while (preVertexArr[index] != -1) {
                  index = preVertexArr[index];
                  strategy += " - " + vertexArr[index];
              }
              strategies[i] = strategy;
          }
  
          //打印路线和距离
          System.out.println("路线 : 距离");
          for (int i=0; i<distanceArr.length; i++) {
              System.out.println(strategies[i] + " : " + distanceArr[i]);
          }
      }
  }

• （3）代码测试

  @Test
  public void dijkstraTest() {
  	//创建图
  	Graph graph = getData();
  	//创建最短路径问题类
  	ShortestPath shortestPath = new ShortestPath(graph);
  	//调用迪杰斯特拉算法
  	shortestPath.dijkstra("G");
  }
  
  
  /**
   * 获取数据（邻接矩阵）
   * @return Graph
   */
  public Graph getData() {
  	String[] vertexes = new String[]{"A", "B", "C", "D", "E", "F", "G"};
  
  	Graph graph = new Graph(vertexes);
  	graph.connect("A", "B", 5);
  	graph.connect("A", "C", 7);
  	graph.connect("A", "G", 2);
  	graph.connect("B", "D", 9);
  	graph.connect("B", "G", 3);
  	graph.connect("C", "E", 8);
  	graph.connect("D", "F", 4);
  	graph.connect("E", "F", 5);
  	graph.connect("E", "G", 4);
  	graph.connect("F", "G", 6);
  
  	return graph;
  }

---

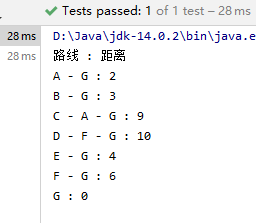
3 弗洛伊德算法

3.1 介绍

弗洛伊德（Floyd）算法：也是最短路径算法之一。弗洛伊德算法中，每一个顶点都是初始顶点，求出每个顶点到其他顶点的最短路径。这也是弗洛伊德算法的特点，会求出所有顶点到其他顶点的最短路径。

3.2 思路

• （1） 创建两个二维数组（矩阵），一个是距离矩阵，用来记录每个顶点之间的最短距离。一个是中间关系矩阵，记录一个顶点到另外一个顶点，是经过哪个中间点。

• （2） 初始化两个矩阵，距离矩阵初始化为图的邻接矩阵，但邻接矩阵用0代表两顶点不连通，距离矩阵使用-1表示。中间关系矩阵，初始化为每一行的中间点为自己

• （3） 按顺序选第一个顶点作为中间顶点，选出所有可能的情况（两层for循环，分别枚举列出起始点和终点，只要起始点到中间点 和 中间点到终点 的距离矩阵的值都不为-1，即为可以连通），并修改距离矩阵和中间关系矩阵

• （4） 重复步骤3，直到所有顶点作为中间点的情况都全部列举出来

3.3 图解

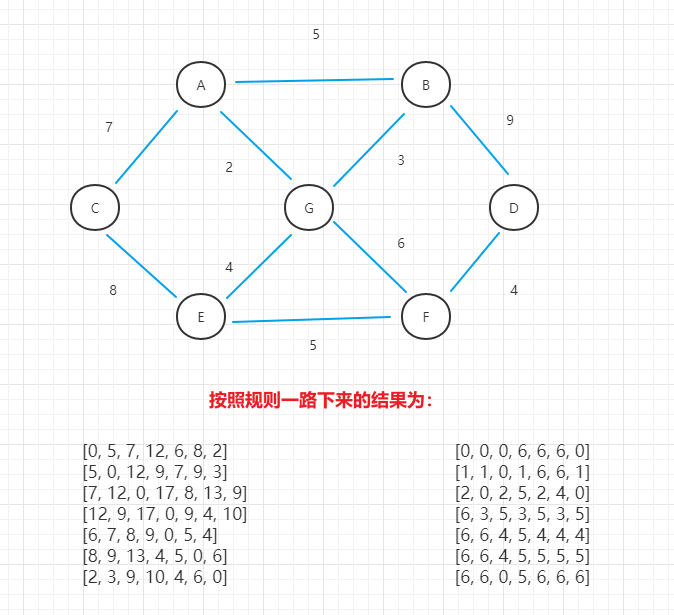
• （1）以此图为例

• （2）创建两个矩阵（距离矩阵和中间关系矩阵），并初始化

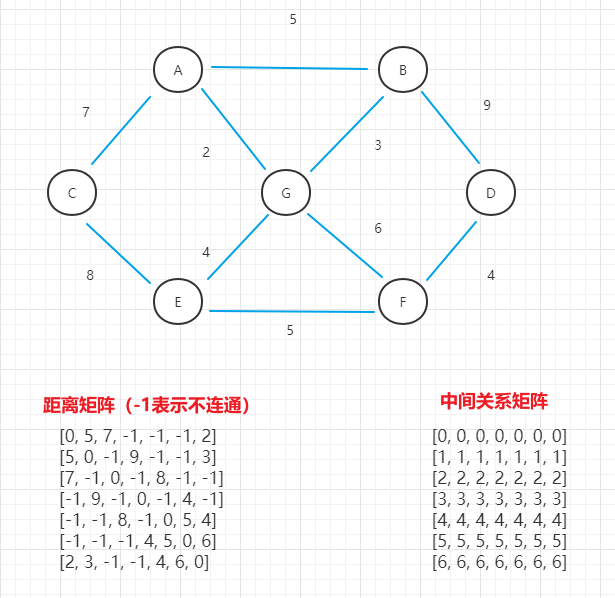
• （3）选A点作为中间顶点，列选出所有可能情况，并修改距离矩阵和中间关系矩阵

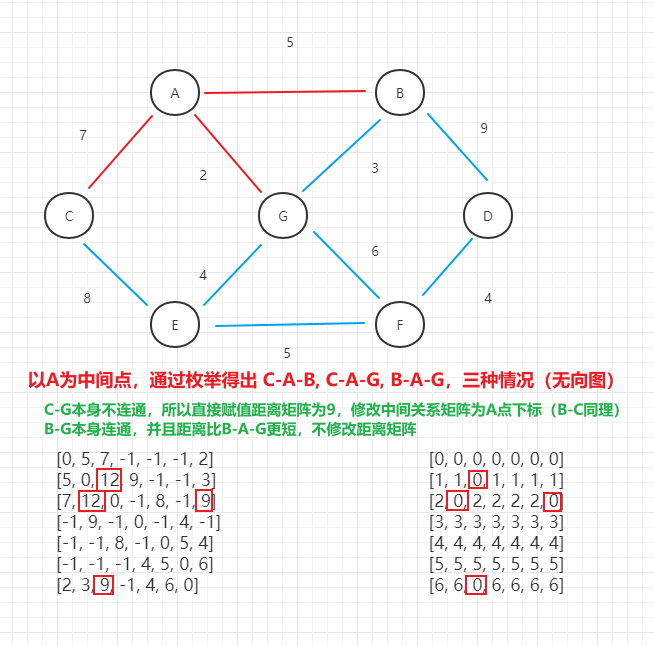
• （4）按照规则得出的最终结果为：

3.4 代码

• （1）图类，上面迪杰斯特拉算法中有，不多赘述

• （2）弗洛伊德算法

  /**
   * 最短路径问题 - 弗洛伊德算法
   * @author letere
   * @create 2021-06-17 22:52
   */
  public class ShortestPath2 {
      //顶点数组
      private final String[] vertexArr;
      //邻接矩阵
      private final int[][] matrix;
  
      //构造器
      public ShortestPath2(Graph graph) {
          this.vertexArr = graph.getVertexes();
          this.matrix = graph.getMatrix();
      }
  
  
      /**
       * 弗洛伊德算法
       */
      public void floyd() {
          int size = vertexArr.length;
  
          //距离矩阵（记录每个点之间的最短距离）
          int[][] distanceMatrix = Arrays.copyOf(matrix, size);
          //除了自己到自己距离为0，其余用-1表示两点不连通
          for (int i=0; i<size; i++) {
              for (int j=i+1; j<size; j++) {
                  if (distanceMatrix[i][j] == 0) {
                      distanceMatrix[i][j] = -1;
                      distanceMatrix[j][i] = -1;
                  }
              }
          }
  
          //中间关系矩阵（记录每个点之间的中间点）
          int[][] midRelationMatrix = new int[size][size];
          //初始化每行的中间点为自己（例：[0, 0, 0], [1, 1, 1], [2, 2, 2]）
          for (int i=0; i<size; i++) {
              for (int j=0; j<size; j++) {
                  midRelationMatrix[i][j] = i;
              }
          }
  
          int len;
          //三次for循环，第一层选中间点，第二层选起始点，第三层选终点
          for (int midIndex=0; midIndex<size; midIndex++) {
              start:for (int startIndex=0; startIndex<size; startIndex++) {
                  for (int endIndex=0; endIndex<size; endIndex++) {
                      //如果中间点与起始点不连通，直接选出下一个起始点
                      if (distanceMatrix[midIndex][startIndex] == -1) {
                          continue start;
                      }
                      //如果中间点与终点不连通，直接选出下一个终点
                      if (distanceMatrix[midIndex][endIndex] == -1) {
                          continue;
                      }
  
                      //都连通，则计算距离（起始点到中间点距离 + 中间点到终点距离）
                      len = distanceMatrix[midIndex][startIndex] + distanceMatrix[midIndex][endIndex];
  
                      //此路径为第一次连通 或 此连通路径更短，则更新距离矩阵和中间关系矩阵
                      if (distanceMatrix[startIndex][endIndex] == -1 || len < distanceMatrix[startIndex][endIndex]) {
                          distanceMatrix[startIndex][endIndex] = len;
                          midRelationMatrix[startIndex][endIndex] = midIndex;
                      }
                  }
              }
          }
  
          //打印结果
          print(distanceMatrix, midRelationMatrix);
      }
  
  
      /**
       * 结果打印
       * @param distanceMatrix 距离矩阵
       * @param midRelationMatrix 中间关系矩阵
       */
      private void print(int[][] distanceMatrix, int[][] midRelationMatrix) {
          int size = distanceMatrix.length;
          for (int startIndex=0; startIndex<size; startIndex++) {
              System.out.println("顶点" + vertexArr[startIndex] + "到各顶点的路线与距离：");
  
              for (int endIndex=0; endIndex<size; endIndex++) {
                  //（1）打印路线
                  //打印起始点
                  System.out.print(vertexArr[startIndex] + " -> ");
                  //打印中间点
                  int temp = startIndex;
                  while (midRelationMatrix[temp][endIndex] != temp) {
                      temp = midRelationMatrix[temp][endIndex];
                      System.out.print(vertexArr[temp] + " -> ");
                  }
                  //打印终点
                  System.out.print(vertexArr[endIndex] + " : ");
  
                  //（2）打印距离
                  System.out.println(distanceMatrix[startIndex][endIndex]);
              }
  
              System.out.println("--------------------------------------");
          }
      }
  }

• （3）测试

  @Test
  public void floydTest() {
  	Graph graph = getData();
  
  	ShortestPath2 shortestPath2 = new ShortestPath2(graph);
  
  	shortestPath2.floyd();
  }
  
  
  /**
   * 获取数据（邻接矩阵）
   * @return Graph
   */
  public Graph getData() {
  	String[] vertexes = new String[]{"A", "B", "C", "D", "E", "F", "G"};
  
  	Graph graph = new Graph(vertexes);
  	graph.connect("A", "B", 5);
  	graph.connect("A", "C", 7);
  	graph.connect("A", "G", 2);
  	graph.connect("B", "D", 9);
  	graph.connect("B", "G", 3);
  	graph.connect("C", "E", 8);
  	graph.connect("D", "F", 4);
  	graph.connect("E", "F", 5);
  	graph.connect("E", "G", 4);
  	graph.connect("F", "G", 6);
  
  	return graph;
  }