【数据结构和算法】马踏棋盘算法

算法之马踏棋盘算法的介绍和实现（马踏棋盘也称为骑士周游算法）

1 马踏棋盘算法

1.1 问题

1.2 算法介绍

马踏棋盘问题（骑士周游问题）：实际上是图的深度优先搜索的应用（递归回溯）

实现思想：需要一个步骤矩阵，记录马每一步的移动的位置。需要计算马可以走的日字可移动位置集合，选其中一点进行递归（当前可移动位置，重新计算下一个可移动位置，有从其中选一个进行递归），直到马移动的步数=棋盘的大小结束递归。反之则进行递归回溯，回到上一个点，重新选另一个可移动的位置

1.3 代码实现

（1）棋盘类

/**
 * 棋盘类
 * @author letere
 * @create 2021-06-18 17:44
 */
public class Chessboard {
    /**
     * 子类：位置类（坐标）
     */
    private static class Location{
        public int x; //横坐标
        public int y; //纵坐标

        public Location(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

//-----------------------------------------

    //棋盘大小
    private static int size;

    //是否完成（用于跳出递归）
    private static boolean isFinish = false;


    /**
     * 运行“马踏棋盘”算法
     * @param x 行
     * @param y 列
     */
    public static void run(int x, int y, int boardSize) {
        //设置棋盘大小        
		size = boardSize;

        //创建步骤矩阵
        int[][] stepMatrix = new int[size][size];

        int step = 1;

        //马踏棋盘-递归
        travel(stepMatrix, x, y, step);

        //打印结果
        if (isFinish) {
            System.out.println("步骤矩阵为：");
            for (int[] row : stepMatrix) {
                for (int column : row) {
                    System.out.print(column + "\t");
                }
                System.out.println();
            }
        }
    }


    /**
     * "马踏棋盘"算法 - 递归本体
     * @param stepMatrix 步骤矩阵
     * @param x 行
     * @param y 列
     * @param step 步骤
     */
    private static void travel(int[][] stepMatrix, int x, int y, int step) {
        //将当前位置步骤记录
        stepMatrix[x][y] = step;

        //计算可移动位置
        List<Location> moveLocations = getMoveLocations(new Location(x, y));

        //遍历可移动位置
        for (Location location : moveLocations) {
            //判断该位置是否已访问，未访问则递归寻找下一个位置
            if (stepMatrix[location.x][location.y] == 0) {
                travel(stepMatrix, location.x, location.y, step+1);
            }
        }

        //递归遍历完毕后，判断是否全部完成
        //未完成则进行还原（回溯）
        if (step < size * size && !isFinish) {
            stepMatrix[x][y] = 0;
        }else {
            isFinish = true;
        }
    }


    /**
     * 计算“马”走日字的可移动位置
     * @param current 当前位置
     * @return List<Location>
     */
    private static List<Location> getMoveLocations(Location current) {
        //可移动位移数组
        List<Location> locations = new ArrayList<>();

        //位移量（左右1，上下2）（左右2， 上下1）
        int[][] displacements = new int[][]{{1, 2}, {2, 1}};
        //方向（正负）
        int[] directions = new int[]{-1, 1};

        //左1右1，上2下2；左2右2，上1下1；八种情况枚举出来，判断是否可以移动
        int x;
        int y;
        for (int[] displacement : displacements) {
            for (int xDirection : directions) {
                for (int yDirection : directions) {
                    x = current.x + displacement[0] * xDirection;
                    y = current.y + displacement[1] * yDirection;

                    //移动后的位置不越界，计入可移动位置中
                    if ((x > -1 && x < size) && (y > -1 && y < size)) {
                        locations.add(new Location(x, y));
                    }
                }
            }
        }

        return locations;
    }
}

（2）测试

@Test
public void chessboardTest() {
    //从(0, 0)为开始长度为8*8大小的棋盘
    Chessboard.run(0, 0, 8);
}

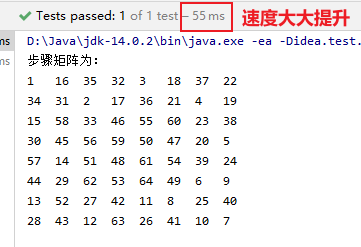
1.4 算法优化

由于算法中递归回溯会浪费很多时间，所以对算法的优化目标在尽量减少递归回溯的出现

可以对可移动位置进行排序，对当前可移动位置的下一个可移动位置个数按升序排序。下一个可移动位置个数少，假若当前的位置不是正确答案，可以以少量的回溯就可以换下一个位置，来求正确答案，从而减少求出正确答案时的递归回溯。（贪心算法思想：每次选最优）

（1）优化代码：新增排序方法，在遍历可移动位置时先进行排序

/**
 * 对位置进行排序（当前位置的可移动位置数量进行升序排序 - 从小到大）
 * @param locations 位置集合
 */
private static void sort(List<Location> locations) {
	//创建比较器，实现比较方法
	Comparator<Location> comparator = new Comparator<>() {
		@Override
		public int compare(Location o1, Location o2) {
			return getMoveLocations(o1).size() - getMoveLocations(o2).size();
		}
	};

	//排序
	locations.sort(comparator);
}


/**
 * "马踏棋盘"算法 - 递归本体
 * @param stepMatrix 步骤矩阵
 * @param x 行
 * @param y 列
 * @param step 步骤
 */
private static void travel(int[][] stepMatrix, int x, int y, int step) {
	//将当前位置步骤记录
	stepMatrix[x][y] = step;

	//计算可移动位置
	List<Location> moveLocations = getMoveLocations(new Location(x, y));
	//按照下一个可移动位置个数进行升序排序
	sort(moveLocations);

	//遍历可移动位置
	for (Location location : moveLocations) {
		//判断该位置是否已访问，未访问则递归寻找下一个位置
		if (stepMatrix[location.x][location.y] == 0) {
			travel(stepMatrix, location.x, location.y, step+1);
		}
	}

	//递归遍历完毕后，判断是否全部完成
	//未完成则进行还原（回溯）
	if (step < size * size && !isFinish) {
		stepMatrix[x][y] = 0;
	}else {
		isFinish = true;
	}
}

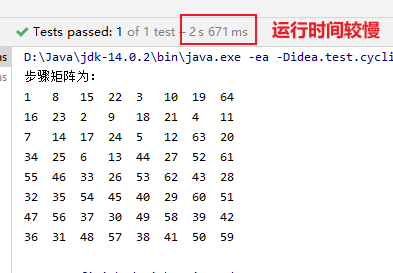
（2）测试

@Test
public void chessboardTest() {
	Chessboard.run(0, 0, 8);
}